题目内容
由定积分的性质和几何意义,说明下列各式的值:
(1)
dx;
(2)
[
-x]dx.
(1)
| ∫ | a -a |
| a2-x2 |
(2)
| ∫ | 1 0 |
| 1-(x-1)2 |
考点:定积分
专题:计算题,选作题
分析:(1)根据定积分定义直接计算即可;
(2)将定积分分为两个积分的和,再分别求出定积分,即可得到结论.
(2)将定积分分为两个积分的和,再分别求出定积分,即可得到结论.
解答:
解:(1)
dx表示以(0,0)为圆心,以
为半径的圆的面积的一半,
即
dx=
a2.
(2)
[
-x]dx=
dx+
(-x)dx …(*)
∵
dx表示以(1,0)为圆心,以1为半径的圆的面积的四分之一.
∴
dx=
.
故(*)的值为
+
d(-
)=
-
.
故
[
-x]dx=
-
.
| ∫ | a -a |
| a2-x2 |
|
即
| ∫ | a -a |
| a2-x2 |
| π |
| 2 |
(2)
| ∫ | 1 0 |
| 1-(x-1)2 |
| ∫ | 1 0 |
| 1-(x-1)2 |
| ∫ | 1 0 |
∵
| ∫ | 1 0 |
| 1-(x-1)2 |
∴
| ∫ | 1 0 |
| 1-(x-1)2 |
| π |
| 4 |
故(*)的值为
| π |
| 4 |
| ∫ | 1 0 |
| x2 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
故
| ∫ | 1 0 |
| 1-(x-1)2 |
| π |
| 4 |
| 1 |
| 2 |
点评:本题考查定积分的几何意义,考查定积分的计算,考查定积分的性质,属于基础题.

练习册系列答案
相关题目
已知集合A={y|y=sinx},B={x|(x+3)(2x-1)≤0},则A∩B=( )
A、[-3,
| ||
B、[-1,
| ||
C、[-1,
| ||
D、(-3,
|
在三棱锥A-BCD的各边AB,BC,CD,DA上分别取E,F,G,H四点,如果EF∩HG=P,则点P( )
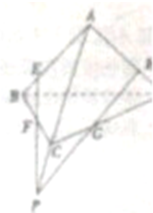

| A、一定在直线BD上 |
| B、一定在直线AC上 |
| C、在直线AC或BD上 |
| D、不在直线AC上,也不在直线BD上 |
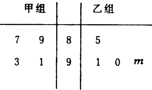 如图所示茎叶图记录了甲、乙两学习小组各4名同学在某次考试中的数学成绩,乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中用m(m∈N)表示.
如图所示茎叶图记录了甲、乙两学习小组各4名同学在某次考试中的数学成绩,乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中用m(m∈N)表示. 如图,平行四边形ABCD中,E、F分别是AD,AB的中点,G为BE与DF的交点.若
如图,平行四边形ABCD中,E、F分别是AD,AB的中点,G为BE与DF的交点.若 如图,椭圆E:
如图,椭圆E: