题目内容
2.已知p:|3x-4|>2,$q:\frac{1}{{{x^2}-x-2}}>0$求¬p是¬q的什么条件.分析 分别求出关于p,q成立的x的范围,结合集合的包含关系判断充分必要性即可.
解答 解:由p:|3x-4|>2,解得:x<$\frac{2}{3}$或x>2,
故¬p:$\frac{2}{3}$≤x≤2,
由q:$\frac{1}{{x}^{2}-x-2}$>0,解得:x<-1或x>2,
故¬q:-1≤x≤2,
所以?p和是?q是充分不必要条件.
点评 本题考查了解不等式问题,考查充分必要条件的定义以及集合的包含关系,是一道基础题.

练习册系列答案
相关题目
13.下列说法正确的是( )
| A. | a∈R,“$\frac{1}{a}$<1”是“a>1”的必要不充分条件 | |
| B. | “p∨q为真命题”的必要不充分条件是“p∧q为真命题” | |
| C. | 命题“?x∈R,使得x2+2x+3<0”的否定是:“?x∈R,x2+2x+3>0” | |
| D. | 命题p:“?x∈R,sinx+cosx≤$\sqrt{2}$”,则¬p是真命题 |
17.方程x2-5x+1=0的两根是两圆锥曲线的离心率,它们是( )
| A. | 椭圆、双曲线 | B. | 椭圆、抛物线 | C. | 双曲线、抛物线 | D. | 无法确定 |
12.若输入的数字是“-3”,输出的结果是( )


| A. | -3 | B. | 13 | C. | 8 | D. | 3 |
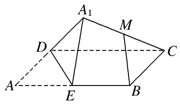 如图,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中,下列说法正确的是①②.(填序号)
如图,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中,下列说法正确的是①②.(填序号)