题目内容
1.(Ⅰ)已知x2+y2=1,求2x+3y的取值范围;(Ⅱ)已知a2+b2+c2-2a-2b-2c=0,求证:$2a-b-c≤3\sqrt{2}$.
分析 (Ⅰ)已知x2+y2=1,由柯西公式(x2+y2)(4+9)≥(2x+3y)2,即可求2x+3y的取值范围;
(Ⅱ)由柯西公式[(a-1)2+(1-b)2+(1-c)2](4+1+1)≥[2(a+1)+(1-b)+(1-c)]2,即可证明结论.
解答 (Ⅰ)解:由柯西公式(x2+y2)(4+9)≥(2x+3y)2,
则|2x+3y|$≤\sqrt{13}$,
∴-$\sqrt{13}$≤2x+3y≤$\sqrt{13}$.
(Ⅱ)证明:由a2+b2+c2-2a-2b-2c=0,得(a-1)2+(1-b)2+(1-c)2=3,
由柯西公式[(a-1)2+(1-b)2+(1-c)2](4+1+1)≥[2(a+1)+(1-b)+(1-c)]2
得证:18≥(2a-b-c)2,所以$2a-b-c≤3\sqrt{2}$.
点评 本题考查柯西公式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
16.为了研究某种细菌在特定环境下随时间变化的繁殖情况,得到如下实验数据:
及y关于t的线性回归方程$\hat y=0.85t-0.25$,则实验数据中m的值为3.
| 天数t(天) | 3 | 4 | 5 | 6 | 7 |
| 繁殖个数y(千个) | 2.5 | m | 4 | 4.5 | 6 |
6.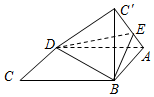 如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则$\frac{AE}{EC′}$=( )
如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则$\frac{AE}{EC′}$=( )
 如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则$\frac{AE}{EC′}$=( )
如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则$\frac{AE}{EC′}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{6}}{6}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}}{3}$ |
13.下列说法正确的是( )
| A. | a∈R,“$\frac{1}{a}$<1”是“a>1”的必要不充分条件 | |
| B. | “p∨q为真命题”的必要不充分条件是“p∧q为真命题” | |
| C. | 命题“?x∈R,使得x2+2x+3<0”的否定是:“?x∈R,x2+2x+3>0” | |
| D. | 命题p:“?x∈R,sinx+cosx≤$\sqrt{2}$”,则¬p是真命题 |
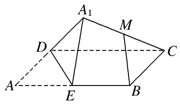 如图,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中,下列说法正确的是①②.(填序号)
如图,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中,下列说法正确的是①②.(填序号)