题目内容
函数y=x2(x>0)的图象在点(ak,ak2)处的切线与x轴交点的横坐标为ak+1,k∈N*,a1=16,则a1+a2+a3= .
考点:
数列递推式.
专题:
计算题.
分析:
先求出函数y=x2在点(ak,ak2)处的切线方程,然后令y=0代入求出x的值,再结合a1的值得到数列的通项公式,再得到a1+a2+a3的值.
解答:
解:在点(ak,ak2)处的切线方程为:y﹣ak2=2ak(x﹣ak),
当y=0时,解得 ![]() ,
,
所以![]() a1+a2+a3=16+8+4=28.
a1+a2+a3=16+8+4=28.
故答案为:28.
点评:
考查函数的切线方程、数列的通项,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
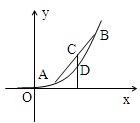 设a,b,λ都为正数,且a≠b,对于函数y=x2(x>0)图象上两点A(a,a2),B(b,b2).
设a,b,λ都为正数,且a≠b,对于函数y=x2(x>0)图象上两点A(a,a2),B(b,b2).