题目内容
在△ABC中，若2sinAsinB＜cos（B-A），则△ABC的形状是
- A.锐角三角形
- B.钝角三角形
- C.直角三角形
- D.等腰三角形
B
分析：把已知不等式的右边利用两角差的余弦函数公式化简后与左边合并，然后再利用两角和的余弦函数公式得到cos（A+B）大于0，根据余弦函数的图象及三角形角的范围得到A+B为锐角，根据内角和定理得到C为钝角，所以三角形为钝角三角形．
解答：依题意，2sinAsinB＜cos（B-A）=cosBcosA+sinAsinB
化简得sinAsinB＜cosAcosB，即cosAcosB-sinAsinB＞0
则cos（A+B）＞0，0＜A+B＜
，所以C为钝角
所以△ABC的形状是钝角三角形，
故选B
点评：此题考查学生灵活运用两角和与差的余弦函数公式化简求值，是一道综合题．做题时应注意角度的范围．
分析：把已知不等式的右边利用两角差的余弦函数公式化简后与左边合并，然后再利用两角和的余弦函数公式得到cos（A+B）大于0，根据余弦函数的图象及三角形角的范围得到A+B为锐角，根据内角和定理得到C为钝角，所以三角形为钝角三角形．
解答：依题意，2sinAsinB＜cos（B-A）=cosBcosA+sinAsinB
化简得sinAsinB＜cosAcosB，即cosAcosB-sinAsinB＞0
则cos（A+B）＞0，0＜A+B＜
，所以C为钝角所以△ABC的形状是钝角三角形，
故选B
点评：此题考查学生灵活运用两角和与差的余弦函数公式化简求值，是一道综合题．做题时应注意角度的范围．
练习册系列答案
出彩同步大试卷系列答案
相关题目
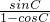的值；