题目内容
若函数f(x)=sin2ωπx(ω>0)的图象在区间[0,
]上至少有两个最高点和两个最低点,则ω的取值范围是 .
| 1 |
| 2 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:先求得函数f(x)=1-
cos2ωπx,根据题意可得区间[0,
]上至少包含
个周期,故有
•
≤
,由此求得ω的范围.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 2π |
| 2ω |
| 1 |
| 2 |
解答:
解:函数f(x)=sin2ωπx=
=1-
cos2ωπx (ω>0)的图象在区间[0,
]上至少有两个最高点和两个最低点,
则区间[0,
]上至少包含
个周期,故有
•
≤
,求得ω≥3π,
故答案为:[3π,+∞).
| 1-cos2ωπx |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则区间[0,
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 2π |
| 2ω |
| 1 |
| 2 |
故答案为:[3π,+∞).
点评:本题主要考查二倍角公式、余弦函数的图象特征,

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
若向量
=(2,0),
=(0,2),则下列结论不正确的是( )
| a |
| b |
A、
| ||||
B、|
| ||||
C、
| ||||
D、
|
设f(x)=ax5+bsinx+2,在(0,+∞)上f(x)的最大值为8,则在区间(-∞,0)上f(x)有( )
| A、最大值-8 |
| B、最小值-8 |
| C、最大值-6 |
| D、最小值-4 |
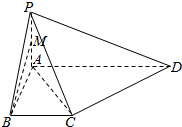 如图,已知PA⊥平面ABCD,AP=AB=BC=
如图,已知PA⊥平面ABCD,AP=AB=BC=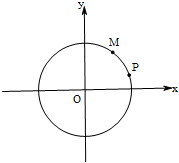 已知圆O:x2+y2=4.
已知圆O:x2+y2=4.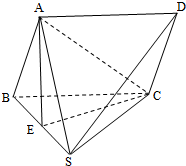 如图,在四棱锥S-ABCD中,底面ABCD是平行四边形,侧SBC是正三角形,点E是SB的中点,且AE⊥平面ABC.
如图,在四棱锥S-ABCD中,底面ABCD是平行四边形,侧SBC是正三角形,点E是SB的中点,且AE⊥平面ABC.