题目内容
(本小题14分)
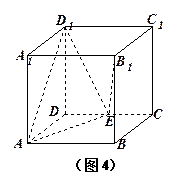
如图4,正方体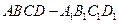 中,点E在棱CD上。
中,点E在棱CD上。
(1)求证: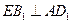 ;
;
(2)若E是CD中点,求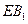 与平面
与平面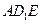 所成的角;
所成的角;
(3)设M在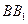 上,且
上,且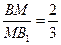 ,是否存在点E,使平面
,是否存在点E,使平面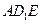 ⊥平面
⊥平面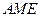 ,若存在,指出点E的位置,若不存在,请说明理由。
,若存在,指出点E的位置,若不存在,请说明理由。
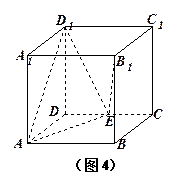
如图4,正方体
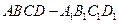 中,点E在棱CD上。
中,点E在棱CD上。(1)求证:
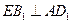 ;
;(2)若E是CD中点,求
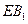 与平面
与平面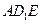 所成的角;
所成的角;(3)设M在
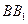 上,且
上,且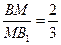 ,是否存在点E,使平面
,是否存在点E,使平面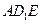 ⊥平面
⊥平面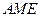 ,若存在,指出点E的位置,若不存在,请说明理由。
,若存在,指出点E的位置,若不存在,请说明理由。略
解:以D为坐标原点,DA,DC, 依次为
依次为 轴、
轴、 轴,
轴, 轴正方向建立空间直角坐标系,并设正方体棱长为1,设点E的坐标为
轴正方向建立空间直角坐标系,并设正方体棱长为1,设点E的坐标为 。 ………2分
。 ………2分
(1) ,
,
∵ ,
,
∴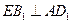 。
。  ………5分
………5分
(2)当E是CD中点时,
 ,
, ,设平面
,设平面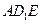 的一个法向量是
的一个法向量是 ,
,
则由 得一组解是
得一组解是 ,………7分
,………7分
又 ,由
,由 ,
,
从而直线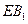 与平面
与平面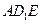 所成的角的正弦值是
所成的角的正弦值是 。 ………9分
。 ………9分
(3)设存在符合题意的E点为E(0,t,0)
 可得平面
可得平面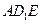 的一个法向量是
的一个法向量是 ,
,
平面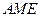 的一个法向量是
的一个法向量是  …11分
…11分
∵ 平面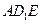 ⊥平面
⊥平面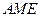 ,
,
∴ ,
,
解得 或
或 (舍), ………13分
(舍), ………13分
故当点E是CD的中点时,平面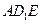 ⊥平面
⊥平面 , ………14分
, ………14分
 依次为
依次为 轴、
轴、 轴,
轴, 轴正方向建立空间直角坐标系,并设正方体棱长为1,设点E的坐标为
轴正方向建立空间直角坐标系,并设正方体棱长为1,设点E的坐标为 。 ………2分
。 ………2分(1)
 ,
,
∵
 ,
,∴
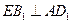 。
。  ………5分
………5分(2)当E是CD中点时,
 ,
, ,设平面
,设平面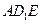 的一个法向量是
的一个法向量是 ,
,则由
 得一组解是
得一组解是 ,………7分
,………7分又
 ,由
,由 ,
,从而直线
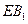 与平面
与平面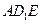 所成的角的正弦值是
所成的角的正弦值是 。 ………9分
。 ………9分(3)设存在符合题意的E点为E(0,t,0)
 可得平面
可得平面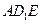 的一个法向量是
的一个法向量是 ,
,平面
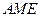 的一个法向量是
的一个法向量是  …11分
…11分∵ 平面
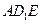 ⊥平面
⊥平面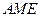 ,
,∴
 ,
,解得
 或
或 (舍), ………13分
(舍), ………13分故当点E是CD的中点时,平面
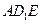 ⊥平面
⊥平面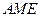 , ………14分
, ………14分
练习册系列答案
相关题目
 中,棱AB=BC=3,
中,棱AB=BC=3, =4,连结
=4,连结 , 在
, 在 上有点E,使得
上有点E,使得 ⊥平面EBD ,BE交
⊥平面EBD ,BE交
 所成角的大小;
所成角的大小;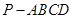 中,底面
中,底面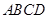 是直角梯形,
是直角梯形,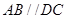 ,
,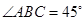 ,
,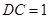 ,
,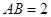 ,
,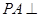 平面
平面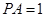 .
. 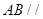 平面
平面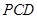 ;
;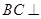 平面
平面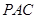 ;
;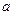 的
的 别是棱BB1、CC1、DD1的中点。
别是棱BB1、CC1、DD1的中点。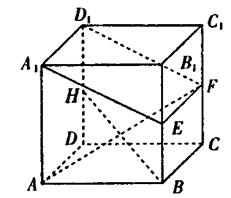
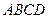 、
、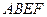 的边长都是1,平面
的边长都是1,平面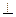 平面
平面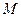 在
在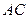 上移动,点
上移动,点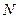 在
在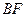 上移动,若
上移动,若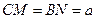 (
(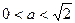 )
)
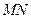 的长;
的长;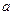 为何值时,
为何值时,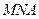 与面
与面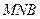 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小.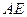 ;
;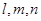 是三条不重合的直线,
是三条不重合的直线, 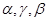 是三个不重合的平面,下列四个命题正确的个数为 ( )
是三个不重合的平面,下列四个命题正确的个数为 ( )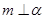 , m∥
, m∥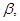
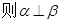
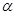 所成的角相等,则m∥n;
所成的角相等,则m∥n;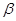 ,n∥β,则
,n∥β,则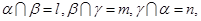
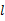 ∥
∥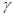 ,则m∥n.
,则m∥n.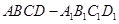 中,
中,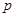 是侧面
是侧面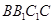 内一动点,若
内一动点,若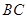 与直线
与直线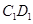 的距离相等,则动点
的距离相等,则动点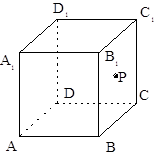
 PA
PA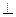 PC,D为AB中点且△PDB为正三角形
PC,D为AB中点且△PDB为正三角形 证:BC⊥平面PAC;
证:BC⊥平面PAC;