题目内容
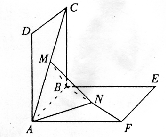
(本题满分14分)如图,正方形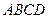 、
、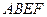 的边长都是1,平面
的边长都是1,平面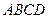
 平面
平面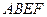 ,点
,点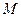 在
在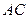 上移动,点
上移动,点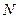 在
在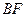 上移动,若
上移动,若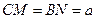 (
(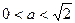 )
)

(I)求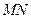 的长;
的长;
(II)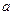 为何值时,
为何值时,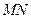 的长最小;
的长最小;
(III)当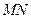 的长最小时,求面
的长最小时,求面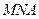 与面
与面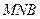 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小.
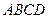 、
、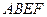 的边长都是1,平面
的边长都是1,平面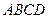
 平面
平面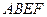 ,点
,点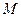 在
在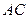 上移动,点
上移动,点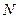 在
在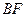 上移动,若
上移动,若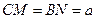 (
(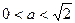 )
)
(I)求
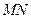 的长;
的长;(II)
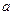 为何值时,
为何值时,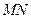 的长最小;
的长最小;(III)当
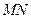 的长最小时,求面
的长最小时,求面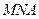 与面
与面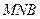 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小.(1)
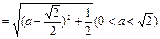
(2)
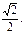
(3)
解:(Ⅰ)作MP∥AB交BC于点P,NQ∥AB交BE于点Q,连结PQ,依题意可得MP∥NQ,且MP=NQ,
即MNQP是平行四边形,∴ MN="PQ."
由已知,CM=BN=a,CB=AB=BE=1,
∴ AC=BF=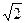 ,
,
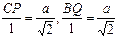
即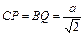
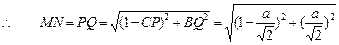
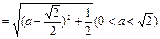 ………………4分
………………4分
(Ⅱ)由(Ⅰ),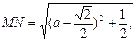 所以,当
所以,当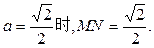
即M、N分别移动到AC、BF的中点时,MN的长最小,最小值为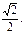 ………………9分
………………9分
(Ⅲ)取MN的中点G,连结AG、BG,
∵ AM=AN,BM=BN,G为MN的中点
∴ AG⊥MN,BG⊥MN,∠AGB即为二面角A-MN-B的平面角,
又AG=BG=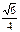 ,所以,由余弦定理有
,所以,由余弦定理有 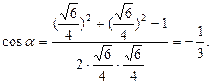
∴ 所求余弦值为
所求余弦值为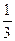 …14分
…14分

即MNQP是平行四边形,∴ MN="PQ."
由已知,CM=BN=a,CB=AB=BE=1,
∴ AC=BF=
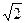 ,
,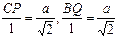
即
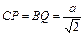
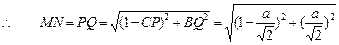
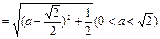 ………………4分
………………4分(Ⅱ)由(Ⅰ),
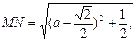 所以,当
所以,当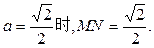
即M、N分别移动到AC、BF的中点时,MN的长最小,最小值为
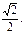 ………………9分
………………9分(Ⅲ)取MN的中点G,连结AG、BG,
∵ AM=AN,BM=BN,G为MN的中点
∴ AG⊥MN,BG⊥MN,∠AGB即为二面角A-MN-B的平面角,
|
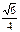 ,所以,由余弦定理有
,所以,由余弦定理有 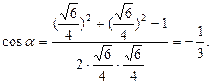
∴
 所求余弦值为
所求余弦值为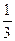 …14分
…14分
练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 C—E的大小。
C—E的大小。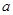 ,高为
,高为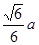 ,则此棱锥的侧面积等于( )
,则此棱锥的侧面积等于( )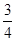
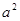
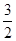
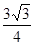

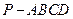 中,
中,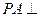 平面
平面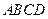 ,底面
,底面 是直角梯形,
是直角梯形,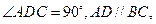
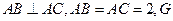 为
为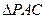
 的重心,
的重心,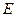 为
为 的中点,
的中点,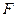 在
在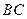 上,且
上,且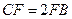 ;
;
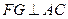 ;
;
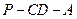 的正切值为多少时,
的正切值为多少时,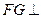 平面
平面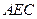 ;
;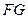 与平面
与平面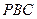 所
所 成角
成角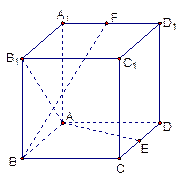
 中,E,F分别是CD,A1D1中点
中,E,F分别是CD,A1D1中点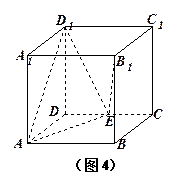
 中,点E在棱CD上。
中,点E在棱CD上。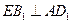 ;
;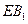 与平面
与平面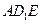 所成的角;
所成的角;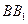 上,且
上,且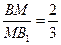 ,是否存在点E,使平面
,是否存在点E,使平面 ,若存在,指出点E的位置,若不存在,请说明理由。
,若存在,指出点E的位置,若不存在,请说明理由。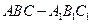 中,侧面
中,侧面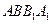 ,
,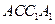 均为正方形,∠
均为正方形,∠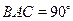 ,点
,点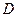 是棱
是棱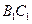 的中点.
的中点.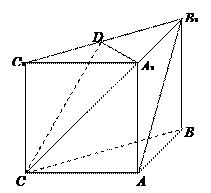
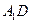 ⊥平面
⊥平面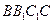 ;
;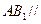 平面
平面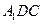 ;
;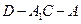 的余弦值
的余弦值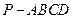 中,顶点
中,顶点 在底面
在底面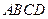 上的射影恰好落在
上的射影恰好落在 的中点
的中点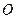 上,又∠
上,又∠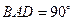 ,
,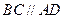 ,且
,且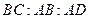
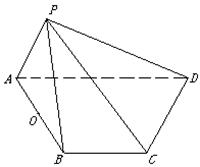
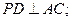
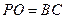 , 求直线
, 求直线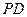 与
与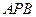 与平面
与平面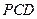 所成的角为
所成的角为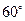 , 求
, 求 的值
的值