题目内容
19.已知Sn为数列{an}的前n项和,若an(4+cosnπ)=n(2-cosnπ),则S20=( )| A. | 31 | B. | 122 | C. | 324 | D. | 484 |
分析 an(4+cosnπ)=n(2-cosnπ),可得:n=2k-1时,4+cosnπ=3=2-cosnπ;n=2k时,4+cosnπ=5,2-cosnπ=1,a2k-1=2k-1=n;a2k=$\frac{2k}{5}$=$\frac{n}{5}$.(k∈N*).
解答 解:∵an(4+cosnπ)=n(2-cosnπ),
∵n=2k-1时,4+cosnπ=3=2-cosnπ;n=2k时,4+cosnπ=5,2-cosnπ=1.
a2k-1=2k-1=n;a2k=$\frac{2k}{5}$=$\frac{n}{5}$.
∴a1=1,a2=$\frac{2}{5}$,a3=3,a4=$\frac{4}{5}$,a5=5,….
∴S20=(1+3+…+19)+$(\frac{2}{5}+\frac{4}{5}+…+\frac{20}{5})$
=$\frac{10×(1+19)}{2}$+$\frac{1}{5}$×$\frac{10×(2+20)}{2}$
=122.
故选:B.
点评 本题考查了数列递推关系、等差数列的通项公式与求和公式、三角函数求值,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.计算log25•log32•log53的值为( )
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
10.用数字1,2,3,4,5组成的无重复数字的四位偶数的个数为( )
| A. | 120 | B. | 240 | C. | 24 | D. | 48 |
7.设a=log23.1,b=logπ2,c=log0.52,则( )
| A. | b>a>c | B. | a>b>c | C. | a>c>b | D. | c>b>a |
14.在数列{an}中,a1=1,an+1=$\frac{2{a}_{n}}{{a}_{n}+2}$,则a4等于( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
8.已知函数f(x)=sinx+cosx,且f'(x)=3f(x),则tanx的值是( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
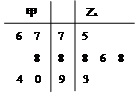 甲乙两位歌手在“中国好声音”选拔赛中,5次得分情况如茎叶图所示,
甲乙两位歌手在“中国好声音”选拔赛中,5次得分情况如茎叶图所示,