Question

15．已知函数f（x）为二次函数，满足f（0）=1，且f（x+1）-f（x）=2x．
（1）求函数f（x）的解析式；
（2）若方程f（2^x）=2^x+a在x∈（-∞，2]上有两个不同的解，求实数a的取值范围．

Answer 1

分析 （1）设出函数f（x）的解析式，根据f（0）=1求出c的值，根据f（x+1）-f（x）=2x，求出a，b的值，从而求出函数的解析式即可；
（2）问题转化为a=（2^x-1）²在x∈（-∞，2]上有两个不同的解，令t=2^x，则0＜t≤4，令g（t）=（t-1）²，画出函数g（t）和y=a的图象，读出a的范围即可．

解答 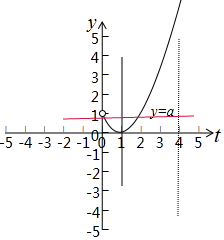解：（1）设f（x）=ax²+bx+c，由f（0）=1得c=1，
∴f（x）=ax²+bx+1，
∴f（x+1）=a（x+1）²+b（x+1）+1=ax²+（2a+b）x+a+b+1，
∴f（x+1）-f（x）=ax²+（2a+b）x+a+b+1-ax²-bx-1
=2ax+a+b，
∵f（x+1）-f（x）=2x，
∴2ax+a+b=2x，
∴2a=2且a+b=0，
∴a=1，b=-1，
∴f（x）=x²-x+1；
（2）若方程f（2^x）=2^x+a在x∈（-∞，2]上有两个不同的解，
即a=（2^x-1）²在x∈（-∞，2]上有两个不同的解，
令t=2^x，则0＜t≤4，
令g（t）=（t-1）²，
画出函数g（t）和y=a的图象，如图所示：
故0＜a＜1．

点评 本题考查了二次函数的性质，考查指数函数的性质以及函数的零点问题，考查转化思想，数形结合思想，是一道中档题．