题目内容
不等式4x2-4x+1>0的解集为
- A.R=(-∞,+∞)
- B.∅
- C.{
 }
} - D.{x
 }
}
D
分析:根据一元二次不等式的解法和实数的性质即可得出.
解答:∵4x2-4x+1>0,∴(2x-1)2>0,∴2x-1≠0,即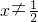 ,∴原不等式的解集为{x|
,∴原不等式的解集为{x|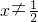 }.
}.
故选D.
点评:熟练掌握一元二次不等式的解法和实数的性质是解题的关键.
分析:根据一元二次不等式的解法和实数的性质即可得出.
解答:∵4x2-4x+1>0,∴(2x-1)2>0,∴2x-1≠0,即
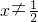 ,∴原不等式的解集为{x|
,∴原不等式的解集为{x|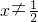 }.
}.故选D.
点评:熟练掌握一元二次不等式的解法和实数的性质是解题的关键.

练习册系列答案
相关题目