题目内容
12.设点P分有向线段$\overrightarrow{{P}_{1}{P}_{2}}$的比是λ,且点P在有向线段$\overrightarrow{{P}_{1}{P}_{2}}$的延长线上,则λ的取值范围是( )| A. | (-∞,-1) | B. | (-1,0) | C. | (-∞,0) | D. | (-∞,-$\frac{1}{2}$) |
分析 根据定比分点的定义,结合题意画出图形,即可求出λ的取值范围.
解答 解:点P分有向线段$\overrightarrow{{P}_{1}{P}_{2}}$的比是λ,
且点P在有向线段$\overrightarrow{{P}_{1}{P}_{2}}$的延长线上,如图所示;
所以|$\overrightarrow{{P}_{1}P}$|>|$\overrightarrow{{PP}_{2}}$|,
即λ=$\frac{\overrightarrow{{P}_{1}P}}{\overrightarrow{{PP}_{2}}}$<-1,
∴λ的取值范围是(-∞,-1).
故选:A.
点评 本题考查了定比分点的概念与应用问题,是基础题目.

练习册系列答案
相关题目
3.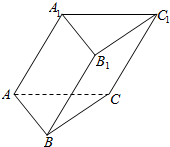 如图,在三棱柱ABC-A1B1C1中,各棱长均相等,且∠A1AB=∠A1AC=∠BAC=60°,则AB1与底面ABC所成角的正弦值为( )
如图,在三棱柱ABC-A1B1C1中,各棱长均相等,且∠A1AB=∠A1AC=∠BAC=60°,则AB1与底面ABC所成角的正弦值为( )
 如图,在三棱柱ABC-A1B1C1中,各棱长均相等,且∠A1AB=∠A1AC=∠BAC=60°,则AB1与底面ABC所成角的正弦值为( )
如图,在三棱柱ABC-A1B1C1中,各棱长均相等,且∠A1AB=∠A1AC=∠BAC=60°,则AB1与底面ABC所成角的正弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
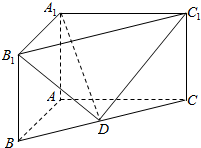 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=2,AC=4,AA1=3,D是BC的中点,求直线DB1与平面A1C1D所成角的正弦值.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=2,AC=4,AA1=3,D是BC的中点,求直线DB1与平面A1C1D所成角的正弦值.