题目内容
19.定义在R上的函数f(x)=ax3+bx2+cx+3同时满足以下条件:①f(x)在(-∞,-1)上是增函数,在(-1,0)上是减函数;
②f(x)的导函数是偶函;
③f(x)在x=0处的切线与第一、三象限的角平分线垂直.
求函数y=f(x)的解析式.
分析 由函数的三个性质可得abc的方程组,解方程组可得.
解答 解:求导数可得f′(x)=3ax2+2bx+c,
由①可得f′(-1)=3a-2b+c=0,
由②可得b=0,
由③可得f′(0)=c=-1,
联立解得a=$\frac{1}{3}$,b=0,c=-1,
∴函数y=f(x)的解析式为f(x)=$\frac{1}{3}$x3-cx+3
点评 本题考查待定系数法求函数解析式,属基础题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
9.抛物线y=$\frac{1}{8}$x2上一点M到焦点的距离为4,则点M的纵坐标为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.若$\underset{lim}{n→∞}$$\frac{f({x}_{0})-f({x}_{0}+△x)}{△x}$=1,则f′(x0)等于( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | -1 |
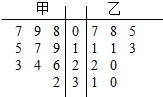 某赛季,甲、乙两名篮球运动员都参加了10场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,若甲运动员的中位数为a,乙运动员的众数为b,则a-b的值是( )
某赛季,甲、乙两名篮球运动员都参加了10场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,若甲运动员的中位数为a,乙运动员的众数为b,则a-b的值是( )