题目内容
设函数 .
.
(1)若函数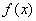 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数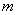 的取值范围;
的取值范围;
(2)若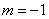 ,试比较当
,试比较当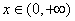 时,
时,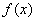 与
与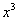 的大小;
的大小;
(3)证明:对任意的正整数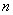 ,不等式
,不等式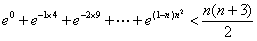 成立.
成立.
解析:(1)∵ 又函数
又函数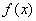 在定义域上是单调函数.
在定义域上是单调函数.
∴  或
或 在
在 上恒成立
上恒成立
若 在
在 上恒成立,即函数
上恒成立,即函数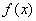 是定义域上的单调地增函数,则
是定义域上的单调地增函数,则 在
在 上恒成立,由此可得
上恒成立,由此可得 ;
;
若 在
在 上恒成立,则
上恒成立,则 在
在 上恒成立.即
上恒成立.即 在
在 上恒成立.
上恒成立.
∵ 在
在 上没有最小值
上没有最小值
∴不存在实数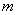 使
使 在
在 上恒成立.
上恒成立.
综上所述,实数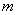 的取值范围是
的取值范围是 .
.
(2)当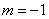 时,函数
时,函数 .
.
令
则
显然,当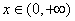 时,
时, ,
,
所以函数 在
在 上单调递减
上单调递减
又 ,所以,当
,所以,当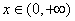 时,恒有
时,恒有 ,
,
即 恒成立.
恒成立.
故当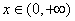 时,有
时,有
(3)数学归纳法
证明:1、当 时,左边=
时,左边= ,右边=
,右边= ,原不等式成立.
,原不等式成立.
2、设当 时,原不等式成立,
时,原不等式成立,
即
则当 时,
时,
左边=
只需证明
即证
即证
由(2)知
即
令 ,即有
,即有
所以当 时成立
时成立
由1、2知,原不等式成立

练习册系列答案
相关题目
 ,若在
,若在 上任取一个实数
上任取一个实数 ,则不等式
,则不等式 成立的概率是( )
成立的概率是( )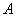 、
、
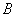 、
、
 、
、
 、
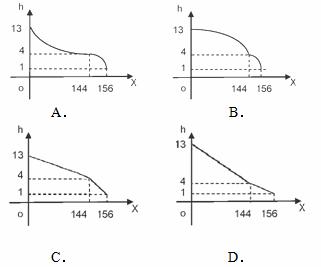
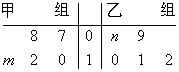
、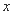 分钟, 瓶内液面与进气管的距离为
分钟, 瓶内液面与进气管的距离为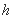 厘米,已知当
厘米,已知当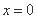 时,
时,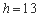 .如果瓶内的药液恰好156分钟滴完. 则函数
.如果瓶内的药液恰好156分钟滴完. 则函数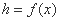 的图像为( )
的图像为( )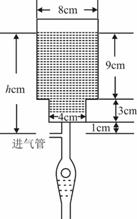
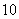 .
.
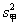 和
和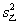 ,并由此分析两组技工的加工水平;
,并由此分析两组技工的加工水平;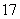 ,则称该车间“质量合格”,求该车间“质量合格”的概率.
,则称该车间“质量合格”,求该车间“质量合格”的概率.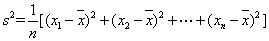 ,其中
,其中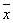 为数据
为数据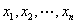 的平均数).
的平均数). 中,
中, .
.  ;
; 的余弦值;
的余弦值; 上是否存在点
上是否存在点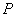 ,使得平面
,使得平面
 平面
平面 ,若存在,求出
,若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
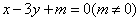 与双曲线
与双曲线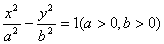 的两条渐近线分别交于点
的两条渐近线分别交于点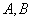 ,若点
,若点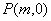 满足
满足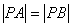 ,则该双曲线的离心率是________.
,则该双曲线的离心率是________. 函数
函数
 有相同极值点.
有相同极值点. 的值;
的值; ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.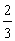 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为 ,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品. ,求
,求 ;
; 为等差数列,
为等差数列, 为其前项和.若
为其前项和.若 ,
, ,则公差
,则公差 ________;
________;