题目内容
已知函数 函数
函数

 有相同极值点.
有相同极值点.
(1)求函数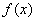 的最大值;
的最大值;
(2)求实数 的值;
的值;
(3)若 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
解析:(1) ,
,
由 得
得 ;由
;由 得
得 .
.

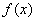 在
在 上为增函数,在
上为增函数,在 上为减函数.
上为减函数.
 函数
函数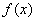 的最大值为
的最大值为 .
.
(2)因为 ,所以
,所以 .
.
由(1)知, 是函数
是函数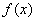 的极值点.又因为函数
的极值点.又因为函数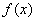 与
与 有相同极值点,
有相同极值点,

 是函数
是函数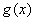 的极值点.
的极值点.
 ,解得
,解得 .
.
经检验,当 时,函数
时,函数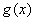 取到极小值,符合题意(6分)
取到极小值,符合题意(6分)
(3)因为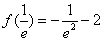 ,
, ,
, ,
,

 ,即
,即 ,
,

 ,
,  ,
, ,
,
由(2)知 ,
,
 .
.

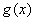 在
在 上,
上, ;当
;当 时,
时, .
.

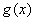 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.

 ,
, ,
, ,而
,而 ,
,

 .
.

 ,
, ,
, ,
,
①当 ,即
,即 时,对于
时,对于 ,不等式
,不等式 恒成立,
恒成立,
即 ,
,

 ,
,
 ,
,
由 得
得 .
.
②当 时,即
时,即 ,对于
,对于 ,不等式
,不等式 恒成立,
恒成立,
即 ,
,

 ,
,

 .
.
综上所述,所求的实数 的取值范围为
的取值范围为 .
.

练习册系列答案
相关题目
 满足
满足 ,数列
,数列 的前n项和为
的前n项和为 ,且
,且 ,则
,则
 ,由下往上的六个点:
,由下往上的六个点: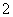 ,
, ,
, ,
, ,
, 的横、纵坐标分别对应数列
的横、纵坐标分别对应数列 (
( )的前
)的前 项,如下表所示:
项,如下表所示: 
 .
.
 .
.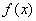 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数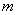 的取值范围;
的取值范围;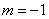 ,试比较当
,试比较当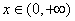 时,
时,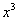 的大小;
的大小;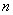 ,不等式
,不等式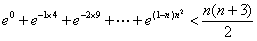 成立.
成立.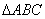 中,三内角
中,三内角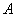 ,
,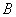 ,
,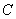 的对边分别为
的对边分别为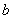 ,
, 且
且 ,
, ,
, 为
为 的最大值为 .
的最大值为 .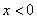 ”是“
”是“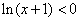 ”的充要条件
”的充要条件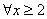 ,
,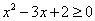 ”的否定是“
”的否定是“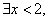
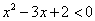 ”
”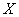 服从正态分布
服从正态分布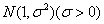 ,若
,若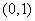 内取值的概率为0.4,则
内取值的概率为0.4,则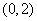 内取值的概率为0.8
内取值的概率为0.8 满足条件:
满足条件: ,则
,则 的最大值是 。
的最大值是 。 、
、 、
、 是三个不同的平面,给出下列命题,正确的是( ).
是三个不同的平面,给出下列命题,正确的是( ). ,
, ,则
,则 B.若
B.若 ,
, ,则
,则 ,则
,则 D.若
D.若 ,
, ,
, ,则
,则
 ,
, ,
, ,则
,则 的大小关系是( )
的大小关系是( )  B.
B. C.
C. D.
D.