题目内容
函数f（x）的部分图象如图所示，则下列选项正确的是
- A.f（x）=x+sinx
- B.f（x）=xcosx
- C.f（x）=x•（x-
）•（x-
） - D.f（x）=
B
分析：通过函数图象判断函数的奇偶性，函数图象经过的特殊点否定选项得到结果即可．
解答：由函数的图象可知，函数是奇函数，而f（x）=x•（x-）•（x-）不是奇函数，所以选项C不正确，
又因为函数图象经过（
）所以f（x）=x+sinx，不满足题意，A不正确，
f（x）=xcosx满足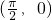
；
f（x）=，满足；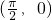
结合函数图象的函数值的范围，x越大时函数值的绝对值接近0，可知，选项D不正确．
故选B．
点评：本题考查函数的图象的应用，函数的奇偶性，函数的最值，考查分析问题解决问题的能力．
分析：通过函数图象判断函数的奇偶性，函数图象经过的特殊点否定选项得到结果即可．
解答：由函数的图象可知，函数是奇函数，而f（x）=x•（x-
）•（x-）不是奇函数，所以选项C不正确，又因为函数图象经过（
）所以f（x）=x+sinx，不满足题意，A不正确，f（x）=xcosx满足
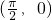；f（x）=
，满足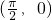；结合函数图象的函数值的范围，x越大时函数值的绝对值接近0，可知，选项D不正确．
故选B．
点评：本题考查函数的图象的应用，函数的奇偶性，函数的最值，考查分析问题解决问题的能力．
练习册系列答案
相关题目
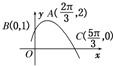已知函数f（x）的部分图象如图所示，则f（x）的解析式可能为（ ）A、f（x）=2cos（
| ||||
B、f（x）=
| ||||
C、f（x）=2sin（
| ||||
D、f（x）=2sin（4x+
|
已知函数f（x）=Asin（ωx+?）（A＞0，ω＞0，0＜?＜π），其导函数f′（x）的部分图象如图所示，则函数f（x）的解析式为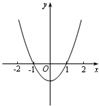
5、已知可导函数f（x）的导函数f′（x）的部分图象如图所示，则函数f（x+1）的部分图象可能是（ ）
函数f（x）的部分图象如图所示，则f（x）的解析式可能是（ ）
（2011•南通模拟）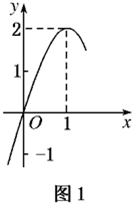
如图所示：图1是定义在R上的二次函数f（x）的部分图象，图2是函数g（x）=loga（x+b）的部分图象．