Question

2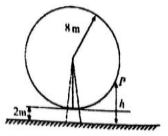．如图，一个摩天轮的半径为8m，每12min旋转一周，最低点离地面为2m，若摩天轮边缘某点P从最低点按逆时针方向开始旋转，则点P离地面的距离h（m）与时间t（min）之间的函数关系是（　　）

• A． h=8cost+10
• B． h=-8cos$\frac{π}{3}$t+10
• C． h=-8sin$\frac{π}{6}$t+10
• D． h=-8cos$\frac{π}{6}$t+10

Answer 1

分析 由实际问题设出P与地面高度与时间t的关系，f（t）=Acos（ωt+φ）+B（A＞0，ω＞0，φ∈[0，2π）），由题意求出三角函数中的参数A，B，及周期T，利用三角函数的周期公式求出ω，通过初始位置求出φ，从而得解．

解答 解：由题意，T=12，
∴ω=$\frac{π}{6}$，
设h（t）=Acos（ωt+φ）+B，（A＞0，ω＞0，φ∈[0，2π）），
则$\left\{\begin{array}{l}{A+B=18}\\{-A+B=2}\end{array}\right.$，
∴A=8，B=10，可得：h（t）=8cos（$\frac{π}{6}$t+φ）+10，
∵P的初始位置在最低点，t=0时，有：h（t）=2，
即：8cosφ+10=2，解得：φ=2kπ+π，k∈Z，
∴φ=π，
∴h与t的函数关系为：h（t）=8cos（$\frac{π}{6}$t+π）+10=-8cos$\frac{π}{6}$t+10，（t≥0），
故选：D．

点评 本题考查通过实际问题得到三角函数的性质，由性质求三角函数的解析式；考查y=Asin（ωx+φ）中参数的物理意义，注意三角函数的模型的应用，属于中档题．