题目内容
如图,Rt△ABC中,∠C=90°,其内切圆切AC边于D点,O为圆心.若|
|=2|
|=2,则
·
= .
-3解析:以CA所在的直线为x轴,CB所在的直线为y轴,建立平面直角坐标系,则C(0,0)、O(1,1)、A(3,0).
设直角三角形内切圆与AB边交于点E,与CB边交于点F,则由圆的切线长定理可得BE=BF,AD=AE=2,设BE=BF=x,在Rt△ABC中,可得CB2+CA2=AB2,即(x+1)2+9=(x+2)2,解得x=3,故B(0,4).
∴·=(1,-3)·(-3,0)=-3.
练习册系列答案
相关题目
sin 
,1),n=(cos 
)的值为( )
(B)
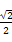(C)-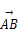
=2e1-8e2,
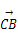=e1+3e2,
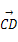=2e1-e2.
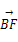=3e1-ke2,且B、D、F三点共线,求k的值.
若
为直角三角形，则必有 （ ）
B．
D．
＝(1,0)，
＝(2,1)，
＝2
＝
＝
，
＝
，
＝
，
＝
，用
、
、
. 
中，已知
，
， 
= .