题目内容
已知数列{an}满足an=
，且f（n）=a1+a2+a3+…+a2n-2+a2n-1，（n∈N*），则f（4）-f（3）的值为 ．
|
考点：数列的求和
专题：等差数列与等比数列
分析：由已知得f（4）-f（3）=（a1+a2+…+a5+a6+a7）-（a1+a2+…+a5）=a6+a7，由此利用an=
，能求出结果．
|
解答：
解：∵数列{an}满足an=
，
且f（n）=a1+a2+a3+…+a2n-2+a2n-1，（n∈N*），
∴f（4）-f（3）=（a1+a2+…+a5+a6+a7）-（a1+a2+…+a5）
=a6+a7
=（62-1）+27
=163．
故答案为：163．
|
且f（n）=a1+a2+a3+…+a2n-2+a2n-1，（n∈N*），
∴f（4）-f（3）=（a1+a2+…+a5+a6+a7）-（a1+a2+…+a5）
=a6+a7
=（62-1）+27
=163．
故答案为：163．
点评：本题考查函数值的求法，是中档题，解题时要注意数列的性质和递推公式的合理运用．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
已知数列{an}的首项a1=1，an+1=
+1，则这个数列的第四项是（ ）
| 2 |
| an |
A、
| ||
B、
| ||
C、
| ||
| D、6 |
三棱锥P-ABC的三条侧棱PA、PB、PC两两互相垂直，且长度分别为3、4、5，则三棱锥P-ABC外接球的体积是（ ）
A、20
| ||||
B、
| ||||
C、
| ||||
| D、50π |
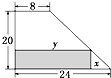（函数的应用）某厂有许多形状为直角梯形的铁皮边角料（如图），为降低消耗，开源节流，现要从这些边角料上截取矩形铁片（如图阴影部分）备用，则截取的矩形面积的最大值为