题目内容
4.已知a,b,c分别是△ABC的角A,B,C所对的边,且C=$\frac{π}{3}$.(1)若c=$\sqrt{3}$a,求sinC+sin(B-A)的值;
(2)若△ABC的面积为$\sqrt{3}$,周长为6,试判断△ABC的形状.
分析 (1)由已知可求得sinC=$\frac{\sqrt{3}}{2}$,由c=$\sqrt{3}$a,利用正弦定理可得:sinC=$\sqrt{3}$sinA,解得sinA=$\frac{1}{2}$,从而可求A,B的值,利用特殊角的三角函数值即可得解.
(2)利用三角形面积公式可求得ab=4,由余弦定理可得c2=(a+b)2-12,又周长为6=a+b+c,解得c2=36+(a+b)2-12(a+b),联立,解得a=b=c=2,从而得解.
解答 解:(1)∵C=$\frac{π}{3}$.sinC=$\frac{\sqrt{3}}{2}$,
∴由c=$\sqrt{3}$a,利用正弦定理可得:sinC=$\sqrt{3}$sinA,解得:sinA=$\frac{1}{2}$,
∴A=$\frac{π}{6}$,B=π-A-C=$\frac{π}{2}$,
∴sinC+sin(B-A)=sin$\frac{π}{3}$+sin($\frac{π}{2}$-$\frac{π}{6}$)=$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
(2)∵C=$\frac{π}{3}$,△ABC的面积为$\sqrt{3}$=$\frac{1}{2}$absinC=$\frac{\sqrt{3}}{4}$ab,解得:ab=4,
∴由余弦定理可得:c2=a2+b2-2abcosC=a2+b2-ab=(a+b)2-3ab=(a+b)2-12,①
又∵周长为6=a+b+c,解得:c=6-(a+b),两边平方可得:c2=36+(a+b)2-12(a+b),②
∴①②联立,解得:(a+b)2-12=36+(a+b)2-12(a+b),整理可得:a+b=4,解得:c=2.
∴解得:a=b=c=2,故三角形为等边三角形.
点评 本题主要考查了三角形面积公式,正弦定理,余弦定理,特殊角的三角函数值在解三角形中的应用,考查了计算能力和转化思想,属于中档题.

| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
| 支持 | 反对 | 合计 | |
| 男性 | 30 | 15 | 45 |
| 女性 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
(2)现从参与调查的女性用户中按分层抽样的方法选出11名发放礼品,在所抽取的11人中分别求出“支持”和“不支持”态度的人数;
(3)将上述调查所得到的频率视为概率,现在从A市所有市民中,采取随机抽样的方法抽取3位市民进行长期跟踪调查,记被抽取的3位市民中持“支持”态度人数为X.
①求X的分布列;
②求X的数学期望E(X)和方差D(X).
附表及公式:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
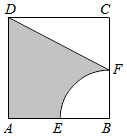 如图所示,在边长为2的正方形ABCD中,圆心为B,半径为1的圆与AB、BC分别交于E,F,则阴影部分绕直线BC旋转一周形成几何体的体积等于( )
如图所示,在边长为2的正方形ABCD中,圆心为B,半径为1的圆与AB、BC分别交于E,F,则阴影部分绕直线BC旋转一周形成几何体的体积等于( )| A. | π | B. | 6π | C. | $\frac{4π}{3}$ | D. | 4π |