题目内容
10．已知$\overrightarrow{a}$=（-2，2），$\overrightarrow{b}$=（x，-3），若$\overrightarrow{a}$⊥$\overrightarrow{b}$，则x的值为（ ）| A． | 3 | B． | 1 | C． | -1 | D． | -3 |
分析 由$\overrightarrow{a}$⊥$\overrightarrow{b}$得到$\overrightarrow{a}$•$\overrightarrow{b}$=-2x+2×（-3）=0，解得即可．
解答 解：∵$\overrightarrow{a}$=（-2，2），$\overrightarrow{b}$=（x，-3），$\overrightarrow{a}$⊥$\overrightarrow{b}$，
∴$\overrightarrow{a}$•$\overrightarrow{b}$=-2x+2×（-3）=0，
解得x=-3，
故选：D．
点评 本题考查了向量垂直与数量积之间的关系，考查了计算能力，属于基础题．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
15．设O是△ABC的外心，a，b，c分别为角A，B，C对应的边，已知b2-2b+c2=0，则$\overrightarrow{{B}C}•\overrightarrow{{A}{O}}$的范围是（ ）
| A． | $（{-\frac{1}{4}，2}]$ | B． | $[{-\frac{1}{4}，2}）$ | C． | $[{-2，\frac{1}{4}}）$ | D． | $（{-2，\frac{1}{4}}]$ |
19．
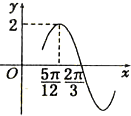已知函数f（x）=2sin（ωx+φ）（ω＞0）的部分图象如图所示，则函数f（x）的一个单调递增区间是（ ）
已知函数f（x）=2sin（ωx+φ）（ω＞0）的部分图象如图所示，则函数f（x）的一个单调递增区间是（ ）| A． | [-$\frac{π}{12}$，$\frac{5π}{12}$] | B． | [-$\frac{7π}{12}$，-$\frac{1}{12}$π] | C． | [-$\frac{π}{12}$，$\frac{7π}{12}$] | D． | [-$\frac{7π}{12}$，$\frac{5π}{12}$] |
20．已知函数f（x）=2sinx的定义域为[a，b]，值域为[-1，2]，则b-a的值不可能是（ ）
| A． | $\frac{2π}{3}$ | B． | π | C． | $\frac{4π}{3}$ | D． | $\frac{5π}{3}$ |