题目内容

4．求下列函数的导数
（1）y=x3+ln（1+x）
（2）y=$\frac{sin2x}{x-2}$．

分析 根据函数的导数公式进行求解即可．

解答 解：（1）函数的导数y′=3x2+$\frac{1}{1+x}$=$\frac{3{x}^{3}+3{x}^{2}+1}{x+1}$，
（2）函数的导数y′=$\frac{2（x-2）cos2x-sin2x}{（x-2）^{2}}$．

点评 本题主要考查函数的导数的计算，根据函数的导数公式是解决本题的关键．

练习册系列答案
相关题目
14．函数$f（x）=\frac{x}{x-1}$的值域是（-∞，1）∪（1，+∞）．
15．已知函数$f（x）=\frac{sin（π+x）cos（π-x）}{{sin（\frac{π}{2}-x）cos（2π+x）}}$．
（1）化简函数f（x）的解析式；
（2）若α为第三象限角且$f（α）=\frac{1}{3}$，求sinα的值．
12．若P（2，1）为圆x2+（y+1）2=25的弦AB的中点，则直线AB的方程是x+y-3=0．
19．已知函数f（x）=cos4x-2sinxcosx-sin4x．
（1）求函数的最小正周期；
（2）求函数的最大值及其相对应的x值．
9．设全集U=R，集合A={x|-2x2+3x+5＞0}，集合B={x|3x2+6≤19x}，求A∪B，A∩B．
16．已知点A（1，-3），B（-5，5），则线段AB中点到直线4x-3y+1=0的距离等于（　　）
A．$\frac{4}{5}$B．$\frac{10}{7}$C．$\frac{12}{5}$D．2
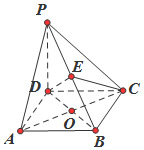13．如图，在四棱锥P-ABCD中，PD⊥平面ABCD，四边形ABCD是菱形，AC=2，BD=2$\sqrt{3}$，且AC，BD交于点O，E是PB上任意一点．
（1）求证：AC⊥DE
（2）已知二面角A-PB-D的余弦值为$\frac{\sqrt{15}}{5}$，若E为PB的中点，求EC与平面PAB所成角的正弦值．
14．如图，函数y=log24x图象上的两点A，B和y=log2x上的点C，线段AC平行于y轴，三角形ABC为正三角形时，点B的坐标为（p，q），则p2×2q=（　　）
A．12B．$12\sqrt{3}$C．6D．$6\sqrt{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网