题目内容
17.已知函数f(x)=sin(ωx+φ)-b(ω>0,0<φ<π)的图象两相邻对称轴之间的距离是$\frac{π}{2}$,若将f(x)的图象先向右平移$\frac{π}{6}$个单位,再向上平移$\sqrt{3}$个单位,所得函数g(x)为奇函数.(1)求f(x)的解析式;
(2)求f(x)的对称轴及单调区间.
分析 (1)由周期求得ω,由函数g(x)为奇函数求得φ和b的值,从而得到函数f(x)的解析式.
(2)令2x+$\frac{π}{3}$=kπ+$\frac{π}{2}$,k∈Z,可解得对称轴,令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈z,求得x的范围,可得到函数的增区间.同理,令2kπ+$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,k∈z,求得x的范围,可得到函数的减区间.
解答 解:(1)∵$\frac{2π}{ω}=2×\frac{π}{2}$,
∴ω=2,
∴f(x)=sin(2x+φ)-b,…(1分)
又∵$g(x)=sin[2(x-\frac{π}{6})+φ]-b+\sqrt{3}$为奇函数,且0<φ<π,则$φ=\frac{π}{3}$,$b=\sqrt{3}$,…(3分)
故$f(x)=sin(2x+\frac{π}{3})-\sqrt{3}$; …(4分)
(2)令2x+$\frac{π}{3}$=kπ+$\frac{π}{2}$,k∈Z,解得:$x=\frac{π}{12}+\frac{kπ}{2}$,k∈Z,
可得对称轴:$x=\frac{π}{12}+\frac{kπ}{2}$,k∈Z,…(6分)
令 2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈z,可得:x∈$[{-\frac{5π}{12}+kπ,\frac{π}{12}+kπ}](k∈Z)$,
可得:增区间为$[{-\frac{5π}{12}+kπ,\frac{π}{12}+kπ}](k∈Z)$,
令2kπ+$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,k∈z,可得:x∈$[{\frac{π}{12}+kπ,\frac{7π}{12}+kπ}](k∈Z)$,
可得:减区间为$[{\frac{π}{12}+kπ,\frac{7π}{12}+kπ}](k∈Z)$.
点评 本题主要考查由函数y=Asin(ωx+∅)的部分图象求解析式,正弦函数的单调性,考查了数形结合思想,属于中档题.

| A. | $±2\sqrt{2}$ | B. | 6 | C. | 2或6 | D. | -2或-6 |
| A. | $\frac{{{{(x+1)}^2}}}{4}-\frac{{{{(y+2)}^2}}}{9}=1$ | B. | $\frac{{{{(x-1)}^2}}}{4}-\frac{{{{(y-2)}^2}}}{9}=1$ | C. | $\frac{{{{(x+1)}^2}}}{4}+\frac{{{{(y+2)}^2}}}{9}=1$ | D. | $\frac{{{{(x-1)}^2}}}{4}+\frac{{{{(y-2)}^2}}}{9}=1$ |
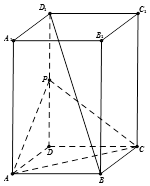 .如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
.如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.