题目内容
已知二次函数f(x)=x2+ax+4,若f(x+1)是偶函数,则实数a的值为 .
考点:二次函数的性质
专题:函数的性质及应用
分析:根据题意可得 f(x+1)=x2+(2+a)x+a+5 是偶函数,故f(x+1)的图象的对称轴为 x=-
=0,由此求得a的值.
| 2+a |
| 2 |
解答:
解:∵二次函数f(x)=x2+ax+4,f(x+1)=x2+(2+a)x+a+5 是偶函数,
故f(x+1)的图象的对称轴为 x=-
=0,解得a=-2,
故答案为:-2.
故f(x+1)的图象的对称轴为 x=-
| 2+a |
| 2 |
故答案为:-2.
点评:本题主要考查二次函数的性质,偶函数的对称轴,属于基础题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
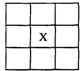 将1,1,2,2,2,3,3,3,3分别填入9个小方格中,每个小方格只填入一个数,每个数填入任何一个小方格是等可能的,则“3”填入图中标有“X”的小方格的概率是( )
将1,1,2,2,2,3,3,3,3分别填入9个小方格中,每个小方格只填入一个数,每个数填入任何一个小方格是等可能的,则“3”填入图中标有“X”的小方格的概率是( )