题目内容
10.商家经销某种商品,原售价为100元/件,每日可售出100件.商家拟降价促销,根据以往经验,若每件降价x,(x∈N*)元,可增加3x件的销售量,则商家应怎样确定降价范围,可使每日销售额比未降价时有所增加?降价多少时每日销售额最大?分析 写出销售额函数f(x)=(100-x)(100+3x),从而作差并化简,从而求范围,再进而求最大值时的x的值.
解答 解:由题意知,
销售额函数f(x)=(100-x)(100+3x),
故f(x)-100×100
=(100-x)(100+3x)-10000
=200x-3x2
=x(200-3x)>0,
故0<x<$\frac{200}{3}$,
即当0<x<$\frac{200}{3}$,x∈N*时,每日销售额用比未降价时有所增加;
而对称轴x=$\frac{200}{3×2}$=$\frac{100}{3}$=33+$\frac{1}{3}$,
故当x=33时,每日的销售额最大.
点评 本题考查了二次函数在实际问题中的应用,同时考查了二次不等式的解法与应用.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
20.若α∈(0,π),且sinα+2cosα=2,则tan$\frac{α}{2}$等于( )
| A. | 3 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
5.已知tan(α+β)=1,tan(α-β)=2,则$\frac{cos2β}{sin2α}$=( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
15.判断下列数列哪一个是等差数列( )
| A. | 1,3,6,10,15,21… | B. | 1,2,4,8,16,32,… | ||
| C. | 1,$\frac{1}{2}$,$\frac{1}{6}$,$\frac{1}{12}$,$\frac{1}{20}$,… | D. | -3,0,3,6,9,12… |
2.在直角坐标系中,P点的坐标为$(\frac{3}{5},\frac{4}{5})$,Q是第三象限内一点,|OQ|=1且$∠POQ=\frac{3π}{4}$,则Q点的横坐标为( )
| A. | $-\frac{{7\sqrt{2}}}{10}$ | B. | $-\frac{{3\sqrt{2}}}{5}$ | C. | $-\frac{{7\sqrt{2}}}{12}$ | D. | $-\frac{{8\sqrt{2}}}{13}$ |
3.执行如图所示的程序框图,则输出S的值为( )
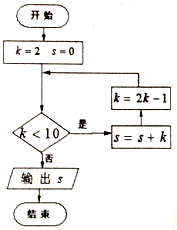

| A. | 10 | B. | 19 | C. | 21 | D. | 36 |