题目内容
2.在直角坐标系中,P点的坐标为$(\frac{3}{5},\frac{4}{5})$,Q是第三象限内一点,|OQ|=1且$∠POQ=\frac{3π}{4}$,则Q点的横坐标为( )| A. | $-\frac{{7\sqrt{2}}}{10}$ | B. | $-\frac{{3\sqrt{2}}}{5}$ | C. | $-\frac{{7\sqrt{2}}}{12}$ | D. | $-\frac{{8\sqrt{2}}}{13}$ |
分析 设∠xOP=α,根据三角函数的坐标法定义,得到α的三角函数值,然后利用三角函数公式求Q的横坐标.
解答 解:设∠xOP=α,则$cosα=\frac{3}{5}$,$sinα=\frac{4}{5}$,${x_Q}=cos(α+\frac{3π}{4})=\frac{3}{5}•(-\frac{{\sqrt{2}}}{2})-\frac{4}{5}•\frac{{\sqrt{2}}}{2}=-\frac{{7\sqrt{2}}}{10}$;
故选:A.
点评 本题考查了三角函数的坐标法定义以及三角函数公式的运用;属于基础题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
9.y=$\frac{1}{2}$sin(6x+1)的最大值( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 6 | D. | 1 |
7.运行图所示的程序,则输出的结果为( )


| A. | 23 | B. | 21 | C. | 19 | D. | 17 |
14.奇函数y=f(x)在区间[2,7]上是增函数,且最小值为-3,那么f(x)在区间[-7,-2]上( )
| A. | 是增函数且最小值为3 | B. | 是增函数且最大值为3 | ||
| C. | 是减函数且最小值为3 | D. | 是减函数且最大值为3 |
12.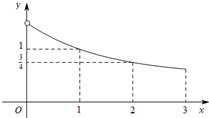 函数f(x) 是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x) 的图象如图所示,那么满足不等式f(x)≥2x-1 的x的取值范围是( )
函数f(x) 是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x) 的图象如图所示,那么满足不等式f(x)≥2x-1 的x的取值范围是( )
 函数f(x) 是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x) 的图象如图所示,那么满足不等式f(x)≥2x-1 的x的取值范围是( )
函数f(x) 是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x) 的图象如图所示,那么满足不等式f(x)≥2x-1 的x的取值范围是( )| A. | [-3,-2]∪[2,3] | B. | [-3,-2]∪(0,1] | C. | [-2,0)∪[1,3] | D. | [-1,0)∪(0,1] |