题目内容
【题目】如图,四边形![]() 是边长为2的菱形,且
是边长为2的菱形,且![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上任意一点.
上任意一点.
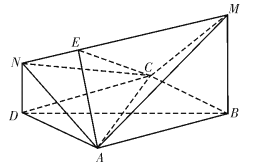
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 的最大值是
的最大值是![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)推导出AC⊥BM,AC⊥BD,从而AC⊥平面BMND,由此能证明平面EAC⊥平面BMND.
(2)由AE=CE>1,cos∠AEC=1![]() ,∠AEC∈(0,π),得到当AE最短时∠AEC最大,即AE⊥MN,CE⊥MN时∠AEC最大,∠AEC是二面角A﹣MN﹣C的平面角,大小是120°,可得AE
,∠AEC∈(0,π),得到当AE最短时∠AEC最大,即AE⊥MN,CE⊥MN时∠AEC最大,∠AEC是二面角A﹣MN﹣C的平面角,大小是120°,可得AE![]() .取MN得中点H,连接H与AC、BD的交点O,由题意知OH⊥平面ABCD,建系,利用向量法结合∠AEC=120°求得ND,利用VM﹣NAC=VM﹣EAC+VN﹣EAC能求出三棱锥M﹣NAC的体积.
.取MN得中点H,连接H与AC、BD的交点O,由题意知OH⊥平面ABCD,建系,利用向量法结合∠AEC=120°求得ND,利用VM﹣NAC=VM﹣EAC+VN﹣EAC能求出三棱锥M﹣NAC的体积.
(1)因为![]() 平面
平面![]() ,则
,则![]() .
.
又四边形![]() 是菱形,则
是菱形,则![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 在平面
在平面![]() 内,所以平面
内,所以平面![]() 平面
平面![]() .
.
(2)设![]() 与
与![]() 的交点为
的交点为![]() ,连结
,连结![]() .因为
.因为![]() 平面
平面![]() ,则
,则![]() ,又
,又![]() 为
为![]() 的中点,则
的中点,则![]() ,所以
,所以![]() ,
,![]() .
.
当![]() 最短时
最短时![]() 最大,此时
最大,此时![]() ,
,![]() ,
,![]() ,
,![]() .
.
取![]() 的中点
的中点![]() ,分别以直线
,分别以直线![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
设![]() ,且a<
,且a<![]() ,
,
则点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,
,
则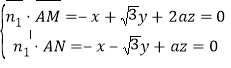 ,
,
取![]() ,则
,则![]() ,
,
同理求得平面![]() 的法向量
的法向量![]() .
.
因为![]() 是二面角
是二面角![]() 的平面角,则
的平面角,则
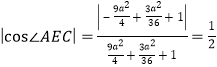 ,解得
,解得![]() 或
或![]() ,又a<
,又a<![]() ,
,
因为![]() ,
,![]() ,
,![]() ,
,
则![]()
![]() .
.


练习册系列答案
相关题目