题目内容
若随机事件A在一次实验中发生的概率为p(0<p<1),用随机变量ξ表示A在三次试验中发生的次数,则
的最大值为 .
| 3Dξ-1 |
| Eξ |
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:由已知条件知ξ~B(3,p),从而得到E(ξ)=3p,D(ξ)=3p(1-p)=3p-3p2,由此利用均值定理能求出
的最大值.
| 3Dξ-1 |
| Eξ |
解答:
解:随机变量ξ的所有可能取值为0,1,
并且有P(ξ=1)=p,P(ξ=0)=1-p,
∴ξ~B(3,p),∴E(ξ)=3p,D(ξ)=3p(1-p)=3p-3p2,
∴
=
=3-(3p+
),
∵0<p<1,
∴3p+
≥2,
当3p=
,p=
时,取“=”,
∴当p=
时,
取得最大值3-2=1.
故答案为:1.
并且有P(ξ=1)=p,P(ξ=0)=1-p,
∴ξ~B(3,p),∴E(ξ)=3p,D(ξ)=3p(1-p)=3p-3p2,
∴
| 3Dξ-1 |
| Eξ |
| 9p-9p2-1 |
| 3p |
| 1 |
| 3P |
∵0<p<1,
∴3p+
| 1 |
| 3p |
当3p=
| 1 |
| 3p |
| 1 |
| 3 |
∴当p=
| 1 |
| 3 |
| 3Dξ-1 |
| Eξ |
故答案为:1.
点评:本题考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型之一,解题时要注意二项分布和均值定理的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
二次不等式ax2+bx+c≥0的解集为空集的条件是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
已知△ABC中,“sinA>
”是“A>
”的( )
| 1 |
| 2 |
| π |
| 6 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
一个树表的生长过程依据图中所示的生长规律,则第15行的实心圆的个数是( )


| A、68 | B、233 |
| C、377 | D、610 |
已知复数z=a+
i在复平面内对应的点位于第二象限,且|z|=2,则复数z等于( )
| 3 |
A、-1+
| ||||
B、1+
| ||||
C、-1+
| ||||
D、-2+
|
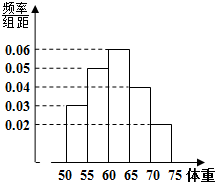 某公司为了了解员工们的健康状况,随机抽取了部分员工作为样本,测量他们的体重(单位:公斤),体重的分组区间为[50,55),[55,60),[60,65),[65,70),[70,75],由此得到样本的频率分布直方图,如图所示.根据频率分布直方图,估计该公司员工体重的众数是
某公司为了了解员工们的健康状况,随机抽取了部分员工作为样本,测量他们的体重(单位:公斤),体重的分组区间为[50,55),[55,60),[60,65),[65,70),[70,75],由此得到样本的频率分布直方图,如图所示.根据频率分布直方图,估计该公司员工体重的众数是