题目内容
15.某班对八校联考成绩进行分析,利用随机数表法抽取样本时,先将70个同学按01,02,03…70进行编号,然后从随机数表第9行第9列的数开始向右读,则选出的第7个个体是( )(注:如表为随机数表的第8行和第9行)
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54.
| A. | 07 | B. | 44 | C. | 15 | D. | 51 |
分析 从随机数表找到第9行第9列数开始向右读,符合条件的是29,64,56,07,52,42,44,问题得以解决.
解答 解:找到第9行第9列数开始向右读,符合条件的是29,64,56,07,52,42,44,
故选出的第7个个体是44,
故选:B.
点评 本题考查随机数表的应用,抽样方法中随机数表的使用,考生不要忽略,在随机数表中每个数出现在每个位置的概率是一样的,所以每个数被抽到的概率是一样的.

练习册系列答案
相关题目
5.如图是某个四面体的三视图,则该四面体的表面积为( )
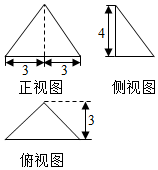

| A. | 12+24$\sqrt{2}$ | B. | 24+24$\sqrt{2}$ | C. | 12+12$\sqrt{2}$ | D. | 24+12$\sqrt{2}$ |
3.执行如图所示的程序框图,则输出的S为( )


| A. | 2 | B. | $\frac{1}{3}$ | C. | -$\frac{1}{2}$ | D. | -3 |
10.已知集合A={x|x2-x-6>0},集合$B=\{y\left|{y=\sqrt{{x^2}+2x+10}}\right.\}$,全集U=R,则(∁UB)∩A为( )
| A. | (-∞,-2) | B. | (2,3) | C. | (3,+∞) | D. | (1,+∞) |
20.函数$f(x)=3sin(2x-\frac{π}{3}+ϕ),ϕ∈(0,π)$满足f(|x|)=f(x),则ϕ的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |