题目内容
8.已知直线ax+by-1=0(ab>0)经过圆x2+y2-2x-4y=0的圆心,则$\frac{1}{a}+\frac{2}{b}$最小值是9.分析 求得圆的圆心,代入直线方程,可得a+2b=1(a,b>0),即有$\frac{1}{a}+\frac{2}{b}$=($\frac{1}{a}+\frac{2}{b}$)×1=($\frac{1}{a}+\frac{2}{b}$)(a+2b)=5+$\frac{2a}{b}$+$\frac{2b}{a}$,运用基本不等式,即可得到最小值.
解答 解:圆x2+y2-2x-4y=0的圆心为(1,2),
由题意可得a+2b=1(a,b>0),
则$\frac{1}{a}+\frac{2}{b}$=($\frac{1}{a}+\frac{2}{b}$)×1=($\frac{1}{a}+\frac{2}{b}$)(a+2b)
=5+$\frac{2a}{b}$+$\frac{2b}{a}$≥5+4=9.
当且仅当a=b=$\frac{1}{3}$时,取得最小值9.
故答案为:9.
点评 本题考查直线和圆的位置关系,注意运用直线过圆心,考查乘1法和均值不等式的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
18.在《张邱建算经》中有一道题:“今有女子不善织布,逐日所织的布同数递减,初日织五尺,末一日织一尺,计织三十日.”由此推断,该女子到第十一日时,大约已经完成三十日织布总量的( )
| A. | 49% | B. | 53% | C. | 61% | D. | 88% |
19.设Sn为等差数列{an}的前n项和,S8=4a3,a7=-2,则a9=( )
| A. | -6 | B. | -4 | C. | -2 | D. | 2 |
20.设变量x,y满足约束条件$\left\{\begin{array}{l}x+y≥2\\ 2x+y≥2\\ x-y≤2\end{array}\right.$目标函数z=x-2y的最大值是( )
| A. | -4 | B. | 2 | C. | $\frac{8}{3}$ | D. | $\frac{16}{3}$ |
17.已知幂函数y=f(x)的图象过点$(2\;,\;\;\sqrt{2})$,则$f({\frac{1}{3}})$的值为( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{1}{3}$ | C. | 3 | D. | 1 |
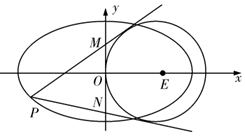 已知椭圆C中心在原点,离心率$\frac{{\sqrt{2}}}{2}$,其右焦点是圆E:(x-1)2+y2=1的圆心.
已知椭圆C中心在原点,离心率$\frac{{\sqrt{2}}}{2}$,其右焦点是圆E:(x-1)2+y2=1的圆心.