题目内容
18.已知复数$z=\frac{3-bi}{i}({b∈R})$的实部和虚部相等,则|z|=( )| A. | 2 | B. | 3 | C. | $2\sqrt{2}$ | D. | $3\sqrt{2}$ |
分析 直接由复数代数形式的乘除运算化简复数z,再结合已知条件求出b的值,根据复数求模公式计算得答案.
解答 解:$z=\frac{3-bi}{i}=\frac{-i(3-bi)}{-{i}^{2}}=-b-3i$,
∵复数$z=\frac{3-bi}{i}({b∈R})$的实部和虚部相等,
∴-b=-3,即b=3.
∴$|z|=\sqrt{(-3)^{2}+(-3)^{2}}=3\sqrt{2}$.
故选:D.
点评 本题考查了复数代数形式的乘除运算,考查了复数模的求法,是基础题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
8.执行如图所示的程序框图,若输出结果是5,则输入的整数p的可能性有( )


| A. | 6种 | B. | 7种 | C. | 8种 | D. | 9种 |
9.复数z=$\frac{(i-1)^{2}+1}{{i}^{2}}$的实部为( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
6.对于数列{an},记Sn=a1+a2+a3+…+an,Πn=a1a2a3…an.在正项等比数列{an}中,a5=$\frac{1}{4}$,a6+a7=$\frac{3}{2}$,则满足Sn>Πn的最大正整数n的值为( )
| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
13.阅读材料:空间直角坐标系O-xyz中,过点P(x0,y0,z0)且一个法向量为$\overrightarrow{n}$=(a,b,c)的平面α的方程为a(x-x0)+b(y-y0)+c(z-z0)=0;过点P(x0,y0,z0)且个方向向量为$\overrightarrow{d}$=(u,v,w)(uvw≠0)的直线l的方程为$\frac{x-{x}_{0}}{u}$=$\frac{y-{y}_{0}}{v}$=$\frac{z-{z}_{0}}{w}$,阅读上面材料,并解决下面问题:已知平面α的方程为3x-5y+z-7=0,直线l是两个平面x-3y+7=0与4y+2z+1=0的交线,则直线l与平面α所成角的大小为( )
| A. | arcsin$\frac{\sqrt{10}}{35}$ | B. | arcsin$\frac{\sqrt{7}}{5}$ | C. | arcsin$\frac{\sqrt{7}}{15}$ | D. | arcsin$\frac{\sqrt{14}}{55}$ |
3.“tanα≠$\sqrt{3}$”是“α≠$\frac{π}{3}$”的( )
| A. | 充分且必要条件 | B. | 既不充分也不必要条件 | ||
| C. | 必要不充分条件 | D. | 充分不必要条件 |
10.满足条件{1,3}∪A={1,3,5}所有集合A的个数是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
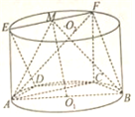 在如图所示的圆柱O1O2中,等腰梯形ABCD内接于下底面圆O1,AB∥CD,且AB为圆O1的直径,EA和FC都是圆柱O1O2的母线,M为线段EF的中点.
在如图所示的圆柱O1O2中,等腰梯形ABCD内接于下底面圆O1,AB∥CD,且AB为圆O1的直径,EA和FC都是圆柱O1O2的母线,M为线段EF的中点.