题目内容
已知椭圆C:
+
=1(a>b>0)的离心率
,其左焦点到点P(2,1)的距离为
,过左焦点作直线OP的垂线l交椭圆C于A,B两点.
(1)求椭圆C的方程;
(2)求△ABP的面积.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 10 |
(1)求椭圆C的方程;
(2)求△ABP的面积.
考点:椭圆的简单性质,椭圆的标准方程
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)运用两点的距离公式,求得c=1,再由离心率公式,可得a,由a,b,c的关系,可得b,进而得到椭圆方程;
(2)设出直线l的方程,联立椭圆方程,消去y,运用韦达定理和弦长公式,及点到直线的距离公式,即可得到面积.
(2)设出直线l的方程,联立椭圆方程,消去y,运用韦达定理和弦长公式,及点到直线的距离公式,即可得到面积.
解答:
解:(1)左焦点(-c,0)到点P(2,1)的距离为
,
则
=
,解得,c=1.
由于椭圆的离心率
,即
=
,即有a=2,b=
=
,
则椭圆的方程为
+
=1;
(2)由于左焦点为(-1,0),直线OP的斜率为
,
则垂线l的斜率为-2,
垂线l的方程为y=-2x-2,
P到l的距离d=
=
,
将l的方程代入椭圆方程,得19x2+32x+4=0,
则有x1+x2=-
,x1x2=
,
则|AB|=
•
=
•
=
.
则△ABP的面积为
d•|AB|=
×
×
=
.
| 10 |
则
| (c+2)2+1 |
| 10 |
由于椭圆的离心率
| 1 |
| 2 |
| c |
| a |
| 1 |
| 2 |
| a2-c2 |
| 3 |
则椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)由于左焦点为(-1,0),直线OP的斜率为
| 1 |
| 2 |
则垂线l的斜率为-2,
垂线l的方程为y=-2x-2,
P到l的距离d=
| |2×2+1+2| | ||
|
| 7 | ||
|
将l的方程代入椭圆方程,得19x2+32x+4=0,
则有x1+x2=-
| 32 |
| 19 |
| 4 |
| 19 |
则|AB|=
| 1+4 |
| (x1+x2)2-4x1x2 |
| 5 |
(
|
=
| 60 |
| 19 |
则△ABP的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 7 | ||
|
| 60 |
| 19 |
42
| ||
| 19 |
点评:本题考查椭圆的方程和性质,考查直线方程和椭圆方程联立,消去未知数,运用韦达定理和弦长公式,考查点到直线的距离公式,考查运算能力,属于基础题.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
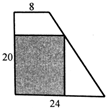 某厂有许多形状为直角梯形的铁皮边角料,如图,上底边长为8,下底边长为24,高为20,为降低消耗,开源节流,现在从这此边角料上截取矩形铁片(如图中阴影部分)备用,则截取的矩形面积最大值为( )
某厂有许多形状为直角梯形的铁皮边角料,如图,上底边长为8,下底边长为24,高为20,为降低消耗,开源节流,现在从这此边角料上截取矩形铁片(如图中阴影部分)备用,则截取的矩形面积最大值为( )