题目内容
设an(n≥2,n∈N*)是 的展开式中x的一次项系数,则
的展开式中x的一次项系数,则 =________.
=________.
17
分析:根据所给的设an(n≥2,n∈N*)是 的展开式中x的一次项系数,写出数列的通项,代入要求的式子,整理出最简形式,得到可以用裂项来求得数列的和形式,求出结果.
的展开式中x的一次项系数,写出数列的通项,代入要求的式子,整理出最简形式,得到可以用裂项来求得数列的和形式,求出结果.
解答:∵an(n≥2,n∈N*)是 的展开式中x的一次项系数,
的展开式中x的一次项系数,
∴an=Cn23n-2,
∴ =
=
= =18(1-
=18(1- +
+
 )=17
)=17
故答案为:17
点评:本题考查二项式的展开式的通项和数列求和,解题的关键是写出数列的通项,把要求的式子整理出可以利用裂项来解的形式.
分析:根据所给的设an(n≥2,n∈N*)是
 的展开式中x的一次项系数,写出数列的通项,代入要求的式子,整理出最简形式,得到可以用裂项来求得数列的和形式,求出结果.
的展开式中x的一次项系数,写出数列的通项,代入要求的式子,整理出最简形式,得到可以用裂项来求得数列的和形式,求出结果.解答:∵an(n≥2,n∈N*)是
 的展开式中x的一次项系数,
的展开式中x的一次项系数,∴an=Cn23n-2,
∴
 =
=
=
 =18(1-
=18(1- +
+
 )=17
)=17故答案为:17
点评:本题考查二项式的展开式的通项和数列求和,解题的关键是写出数列的通项,把要求的式子整理出可以利用裂项来解的形式.

练习册系列答案
相关题目
设an(n≥2,n∈N*)是(3-
)n的展开式中x的一次项的系数,则
(
+
+…+
)=( )
| x |
| lim |
| n→∞ |
| 32 |
| a2 |
| 33 |
| a3 |
| 3n |
| an |
| A、16 | B、17 | C、18 | D、19 |
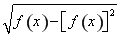
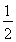
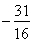
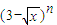 的展开式中x的一次项系数,则
的展开式中x的一次项系数,则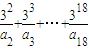 = .
= .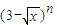 的展开式中x的一次项的系数,则
的展开式中x的一次项的系数,则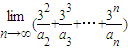 =( )
=( )