题目内容
设an(n≥2,n∈N*)是(3-
)n的展开式中x的一次项的系数,则
(
+
+…+
)=( )
| x |
| lim |
| n→∞ |
| 32 |
| a2 |
| 33 |
| a3 |
| 3n |
| an |
| A、16 | B、17 | C、18 | D、19 |
分析:利用二项展开式的通项公式求出展开式的通项,令x的指数为1求出r的值,将r的值代入通项求出an,
进一步求出
,利用数列求和的方法:裂项法求出极限函数,求出值.
进一步求出
| 3n |
| an |
解答:解:(3-
)n展开式的通项为Tr+1=(-1)r3n-r
x
令
=1得r=2
∴an=3n-2Cn2
∴
=
=18(
-
)
∴
(
+
+…+
)
=18
(1-
+
-
+…+
-
)
=18
(1-
)
=18
故选C
| x |
| C | r n |
| r |
| 2 |
令
| r |
| 2 |
∴an=3n-2Cn2
∴
| 3n |
| an |
| 18 |
| n(n-1) |
| 1 |
| n-1 |
| 1 |
| n |
∴
| lim |
| n→∞ |
| 32 |
| a2 |
| 33 |
| a3 |
| 3n |
| an |
=18
| lim |
| n→∞ |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
=18
| lim |
| n→∞ |
| 1 |
| n |
=18
故选C
点评:解决二项展开式的特定项问题,一般利用二项展开式的通项公式求出通项;求数列的前n项和一般先求出通项,根据通项的特点选择合适的求和方法.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
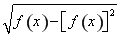
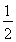
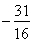
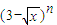 的展开式中x的一次项系数,则
的展开式中x的一次项系数,则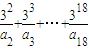 = .
= .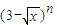 的展开式中x的一次项的系数,则
的展开式中x的一次项的系数,则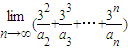 =( )
=( )