题目内容
19.从0-1之间随机地选取两个数,若这两个数对应的点把刻度为0-1之间的线段分成三条,试求分成的这三条线段能构成三角形的概率为$\frac{1}{4}$.分析 先设线段其中两段的长度分别为x、y,分别表示出线段随机地折成3段的x,y的约束条件和3段构成三角形的约束条件,再画出约束条件表示的平面区域,利用面积测度即可求出构成三角形的概率.
解答 解:设三段长分别为x,y,1-x-y,
则总样本区域为 $\left\{\begin{array}{l}{0<x<1}\\{0<y<1}\\{x+y<1}\end{array}\right.$,所表示的平面区域为三角形OAB,其面积为$\frac{1}{2}$,
能构成三角形的事件的区域为 $\left\{\begin{array}{l}{x+y>1-x-y}\\{x+1-x-y>y}\\{y+1-x-y>x}\end{array}\right.$,所表示的平面区域为三角形DEF,其面积为$\frac{1}{8}$,
则所求概率P=$\frac{{S}_{△DEF}}{{S}_{△AOB}}$=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.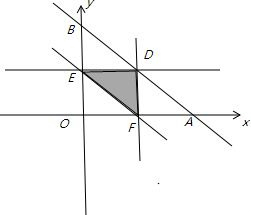
点评 本题考查几何概型概率公式,考查三角形边的关系,考查线性规划的简单应用,考查计算能力,属于中档题.

练习册系列答案
相关题目
8.2010年广东亚运会,某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K和D两个动作,比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员的成绩.假设每个运动员完成每个系列中的两个动作的得分是相互独立的,根据赛前训练统计数据,某运动员完成甲系列和乙系列的情况如表:
甲系列:
乙系列:
(Ⅰ)现该运动员最后一个出场,其之前运动员的最高得分为118分.若该运动员希望获得该项目的第一名,应选择哪个系列,说明理由,并求其获得第一名的概率;
(II)若该运动员选择乙系列,求其成绩X的分布列及其数学期望EX.
甲系列:
| 动作 | K | D | ||
| 得分 | 100 | 80 | 40 | 10 |
| 概率 | $\frac{3}{4}$ | $\frac{1}{4}$ | $\frac{3}{4}$ | $\frac{1}{4}$ |
| 动作 | K | D | ||
| 得分 | 90 | 50 | 20 | 0 |
| 概率 | $\frac{9}{10}$ | $\frac{1}{10}$ | $\frac{9}{10}$ | $\frac{1}{10}$ |
(II)若该运动员选择乙系列,求其成绩X的分布列及其数学期望EX.
