题目内容
4.过点A(6,4)作曲线f(x)=2$\sqrt{x-2}$的切线l,则切线l与x轴及曲线f(x)=2$\sqrt{x-2}$所围成的封闭图形的面积S=$\frac{16}{3}$.分析 求在点(6,4)处的切线方程,欲求封闭图形的面积,利用定积分的几何意义求面积,只须求出积分的上下限即可,故先利用令f(x)=2$\sqrt{x-2}$=0,则x=2.令y=$\frac{1}{2}x+1$=0,则x=-2,再结合图象特征即得,最后定积分公式计算即得.
解答 解:∵f′(x)=$\frac{2}{\sqrt{4x-8}}$,∴f′)6)=$\frac{1}{2}$,
∴切线l的方程为:y-4=$\frac{1}{2}$(x-6),即y=$\frac{1}{2}x+1$
(2)令f(x)=2$\sqrt{x-2}$=0,则x=2.
令y=$\frac{1}{2}x+1$=0,则x=-2.
∴S=${∫}_{-2}^{6}$($\frac{1}{2}x+1$)dx-${∫}_{2}^{6}$(2$\sqrt{x-2}$)dx=$(\frac{1}{4}{x}^{2}+x){|}_{-2}^{6}-\frac{1}{6}(4x-8)^{\frac{3}{2}}{|}_{2}^{6}$=9+6-(1-2)-$\frac{1}{6}×1{6}^{\frac{3}{2}}$=$\frac{16}{3}$.
故答案为$\frac{16}{3}$.
点评 本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程、定积分的几何意义等基础知识,考查运算求解能力.属于中档题.

练习册系列答案
相关题目
13.某校共有17人获得北大、清华保送资格,具体人数如下:
若随机从获取北大、清华保送资格的学生中各取一名,则至少1人是参加数学竞赛的概率为( )
| 竞赛学科 | 数学 | 物理 | 化学 |
| 北大 | 6 | 4 | 2 |
| 清华 | 1 | 0 | 4 |
| A. | $\frac{1}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{15}{34}$ | D. | $\frac{91}{136}$ |
12.圆x2+y2-8x+6y-11=0的圆心、半径是( )
| A. | (4,3),6 | B. | (4,-3),6 | C. | (4,3),36 | D. | (4,-3),36 |
14.设变量x,y满足约束条件:$\left\{\begin{array}{l}{y≥x}\\{x+2y≤2}\\{x≥-2}\end{array}\right.$,则z=$\frac{y+2}{x+2}$ 的( )
| A. | 最大值为-$\frac{1}{2}$ | B. | 最小值为-$\frac{1}{2}$ | C. | 最大值为1 | D. | 最小值为1 |
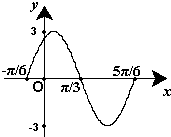 已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的 一段图象(如图)所示.
已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的 一段图象(如图)所示.