题目内容
11.设命题p:函数f(x)=x3+mx2+(m+$\frac{4}{3}$)x+6在R有极值;命题q:3x-9x<m对一切实数x恒成立.
如果命题“p∧q”为假命题,求实数m的取值范围.
分析 如果命题“p∧q”为假命题,则命题p为假,或命题q为假,进而得到实数m的取值范围.
解答 解:若函数f(x)=x3+mx2+(m+$\frac{4}{3}$)x+6在R有极值;
则函数f′(x)=3x2+2mx+(m+$\frac{4}{3}$)的△=$4{m}^{2}-12(m+\frac{4}{3})>0$,
解得:m<-1,或m>4,
即命题p:m<-1,或m>4,
3x-9x<m,即3x-(3x)2<m,即t-t2<m(t>0),
即m>$\frac{1}{2}$,
即命题q:m>$\frac{1}{2}$,
果命题“p∧q”为假命题,
则命题p为假,或命题q为假,
即:-1≤m≤4,或m≤$\frac{1}{2}$,
即m≤4.
点评 本题以命题的真假判断与应用为载体,考查了复合命题,利用导数研究函数的极值,函数恒成立问题等知识点,难度中档.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
20.下列命题:①如果x=y,则sinx=siny;②如果a>b,则a2>b2;③A,B是两个不同定点,动点P满足|PA|+|PB|是常数,则动点P的轨迹是椭圆.其中正确命题的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
6.下列各组函数中表示同一函数的是( )
| A. | $f(x)=x,g(x)={(\sqrt{x})^2}$ | B. | $f(x)=\left|x\right|,g(x)=\sqrt{[}3]{x^3}$ | ||
| C. | $f(x)={x^2},g(x)=\left\{\begin{array}{l}{x^2},(x>0)\\-{x^2},(x<0)\end{array}\right.$ | D. | $f(x)=\frac{{{x^2}-1}}{x-1},g(t)=t+1(t≠1)$ |
20.在等差数列{an}中,a3+a6+a9=27,设数列{an}的前n项和为Sn,则S11=( )
| A. | 18 | B. | 99 | C. | 198 | D. | 297 |
1.某三棱锥的三视图如图所示,正视图是边长为3的等边三角形,则该三棱锥外接球的表面积为( )
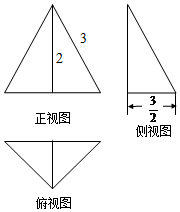

| A. | 12π | B. | $6\sqrt{3}π$ | C. | 9π | D. | 18π |
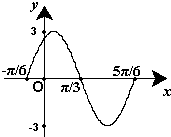 已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的 一段图象(如图)所示.
已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的 一段图象(如图)所示.