题目内容
8.在递减等差数列{an}中,a1a3=${a}_{2}^{2}$-4,若a1=13,则数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和的最大值为( )| A. | $\frac{24}{143}$ | B. | $\frac{1}{143}$ | C. | $\frac{24}{13}$ | D. | $\frac{6}{13}$ |
分析 设公差为d,则d<0,根据题意求出d,得到数列的通项公式,再求出第7项大于0,第8项小于0,再根据裂项求和,即可求出答案.
解答 解:设公差为d,则d<0,
∵a1a3=${a}_{2}^{2}$-4,a1=13,
∴13(13+2d)=(13+d)2-4,
解得d=-2或d=2(舍去),
∴an=a1+(n-1)d=13-2(n-1)=15-2n,
当an=15-2n≥0时,即n≤7.5,
当an+1=13-2n≤0时,即n≥6.5,
∴当n≤7是,an>0
∴$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(15-2n)(13-2n)}$=$\frac{1}{2}$($\frac{1}{2n-15}$-$\frac{1}{2n-13}$)
∴数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和为$\frac{1}{2}$($\frac{1}{-13}$-$\frac{1}{-11}$+$\frac{1}{-11}$-$\frac{1}{-9}$+…+$\frac{1}{2n-15}$-$\frac{1}{2n-13}$)=$\frac{1}{2}$(-$\frac{1}{13}$-$\frac{1}{2n-13}$),
当n=6时,最大,最大值为$\frac{1}{2}$(-$\frac{1}{13}$+1)=$\frac{6}{13}$
故选:D
点评 本题考查了等差数列的通项公式的求法和数列与函数的关系和裂项求和,考查了学生的运算能力和转化能力,属于中档题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
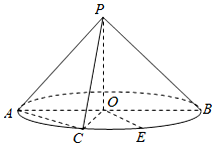 如图,圆锥的底面圆心为O,直径为AB,C为半圆弧AB的中点,E为劣弧CB的中点,且AB=2PO=2$\sqrt{2}$.
如图,圆锥的底面圆心为O,直径为AB,C为半圆弧AB的中点,E为劣弧CB的中点,且AB=2PO=2$\sqrt{2}$.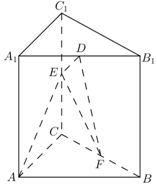 如图,在直棱柱ABC-A1B1C1中,AA1=AB=AC=2,AB⊥AC,D,E,F分别是A1B1,CC1,BC的中点.
如图,在直棱柱ABC-A1B1C1中,AA1=AB=AC=2,AB⊥AC,D,E,F分别是A1B1,CC1,BC的中点. 