题目内容
(本小题满分14分)已知椭圆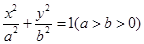 的一个焦点
的一个焦点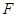 与抛物线
与抛物线 的焦点重合,P为椭圆与抛物线的一个公共点,且|PF|=2,倾斜角为
的焦点重合,P为椭圆与抛物线的一个公共点,且|PF|=2,倾斜角为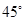 的直线
的直线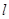 过点
过点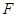 .
.
(1)求椭圆的方程;
(2)设椭圆的另一个焦点为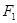 ,问抛物线
,问抛物线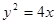 上是否存在一点
上是否存在一点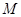 ,使得
,使得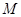 与
与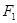 关于直线
关于直线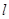 对称,若存在,求出点
对称,若存在,求出点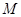 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
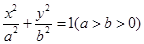 的一个焦点
的一个焦点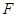 与抛物线
与抛物线 的焦点重合,P为椭圆与抛物线的一个公共点,且|PF|=2,倾斜角为
的焦点重合,P为椭圆与抛物线的一个公共点,且|PF|=2,倾斜角为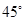 的直线
的直线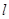 过点
过点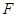 .
.(1)求椭圆的方程;
(2)设椭圆的另一个焦点为
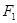 ,问抛物线
,问抛物线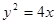 上是否存在一点
上是否存在一点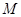 ,使得
,使得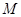 与
与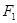 关于直线
关于直线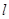 对称,若存在,求出点
对称,若存在,求出点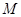 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.(1)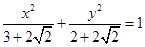 ;
;
(2)抛物线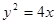 上存在一点
上存在一点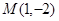 ,使得
,使得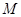 与
与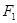 关于直线
关于直线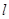 对称.
对称.
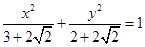 ;
;(2)抛物线
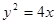 上存在一点
上存在一点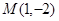 ,使得
,使得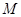 与
与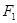 关于直线
关于直线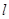 对称.
对称. 试题分析:(1)设P(x,y),因为|PF|=2,根据焦半径公式可求出x=1,代入抛物线方程可求点P的坐标.
再根据椭圆的定义:
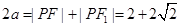 ,求出a,已知c=1,从而可求出
,求出a,已知c=1,从而可求出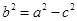 ,故可得椭圆的方程.
,故可得椭圆的方程.(2)先求出直线
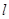 的方程为
的方程为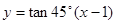 ,即
,即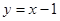 ,再求出椭圆的另一个焦点为
,再求出椭圆的另一个焦点为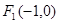 ,可根据点关于直线对称点的求法求出点F1关于直线l的对称点M的坐标,然后代入抛物线方程判定点M是否在抛物线上,从而得到结论.
,可根据点关于直线对称点的求法求出点F1关于直线l的对称点M的坐标,然后代入抛物线方程判定点M是否在抛物线上,从而得到结论.(1)抛物线
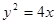 的焦点为
的焦点为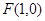 ,………………………1分
,………………………1分设P(x,y)则|PF|=
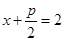 ,故x=1,y=
,故x=1,y=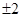 …………………3分
…………………3分∴
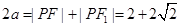 ,
,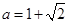 …………………5分
…………………5分∴
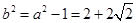 …………………6分
…………………6分∴ 该椭圆的方程为
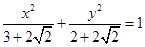 …………………7分
…………………7分(2)∵ 倾斜角为
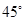 的直线
的直线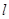 过点
过点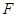 ,
,∴ 直线
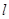 的方程为
的方程为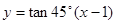 ,即
,即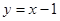 ,…………………8分
,…………………8分由(1)知椭圆的另一个焦点为
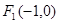 ,设
,设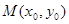 与
与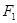 关于直线
关于直线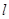 对称,………9分
对称,………9分则得
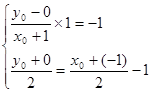 …………………10分
…………………10分解得
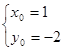 ,即
,即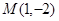 …………………11分
…………………11分又
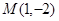 满足
满足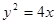 ,故点
,故点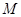 在抛物线上. …………………13分
在抛物线上. …………………13分所以抛物线
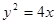 上存在一点
上存在一点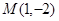 ,使得
,使得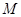 与
与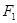 关于直线
关于直线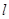 对称.……………14分
对称.……………14分点评:圆锥曲线的定义是重要的解题工具要引起足够重视,利用它解题很多时候起到化繁为简,另辟捷径的作用.解本小题的第二问要掌握点关于直线的对称点的求法.

练习册系列答案
相关题目
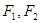 是双曲线
是双曲线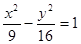 的两个焦点,点
的两个焦点,点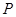 在双曲线上,且
在双曲线上,且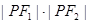
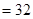 ,求证:
,求证:
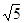 ,离心率为
,离心率为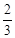 的椭圆的两个焦点分别为F1,F2,过F1作直线交椭圆于A,B两点,则△ABF2的周长为
的椭圆的两个焦点分别为F1,F2,过F1作直线交椭圆于A,B两点,则△ABF2的周长为 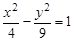 有相同的渐近线,且一条准线为
有相同的渐近线,且一条准线为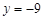 ,求双曲线C的方程;
,求双曲线C的方程; (Ⅱ)已知圆截
(Ⅱ)已知圆截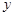 轴所得弦长为6,圆心在直线
轴所得弦长为6,圆心在直线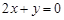 上,并与
上,并与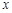 轴相切,求该圆的方程.
轴相切,求该圆的方程.  在坐标轴上,离心率为
在坐标轴上,离心率为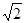 ,且过点(4,-
,且过点(4,-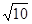 )(1)求双曲线的方程.(2)若点M(3,m)在双曲线上,求证:
)(1)求双曲线的方程.(2)若点M(3,m)在双曲线上,求证: .(3)若点A,B在双曲线上,点N(3,1)恰好是AB的中点,求直线AB的方程(12分)
.(3)若点A,B在双曲线上,点N(3,1)恰好是AB的中点,求直线AB的方程(12分) 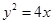 的焦点
的焦点 的直线交抛物线于
的直线交抛物线于 两点,点
两点,点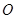 是原点,若
是原点,若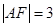 ,则
,则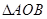 的面积为
的面积为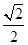



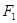 、
、 ,以
,以 为边作正三角形,若双曲线恰好平分另外两边,则双曲线的离心率为( )
为边作正三角形,若双曲线恰好平分另外两边,则双曲线的离心率为( )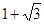
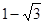

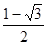
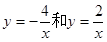 的图象交于点A和点B,若点C是x轴上任意一点,连接AC、BC,
的图象交于点A和点B,若点C是x轴上任意一点,连接AC、BC,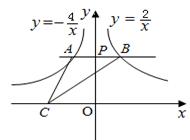
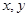 为正实数,
为正实数,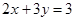 ,则
,则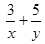 的最小值为 .
的最小值为 .