题目内容
短轴长为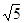 ,离心率为
,离心率为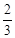 的椭圆的两个焦点分别为F1,F2,过F1作直线交椭圆于A,B两点,则△ABF2的周长为
的椭圆的两个焦点分别为F1,F2,过F1作直线交椭圆于A,B两点,则△ABF2的周长为
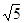 ,离心率为
,离心率为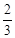 的椭圆的两个焦点分别为F1,F2,过F1作直线交椭圆于A,B两点,则△ABF2的周长为
的椭圆的两个焦点分别为F1,F2,过F1作直线交椭圆于A,B两点,则△ABF2的周长为 | A.24 | B.12 | C.6 | D.3 |
B
试题分析:由已知中短轴长
 ,和离心率
,和离心率 的值得到参数a,b,c的值,分别是a=3,b=2,然后结合题中条件得到三角形△ABF2的周长为椭圆上点到两焦点的距离和的2倍,故为4a=12,进而求解选B
的值得到参数a,b,c的值,分别是a=3,b=2,然后结合题中条件得到三角形△ABF2的周长为椭圆上点到两焦点的距离和的2倍,故为4a=12,进而求解选B点评:解决该试题的关键是分析出所求解的三角形的三边两边的和是符合椭圆的定义的,另一边是焦距,这样可以求解得到。

练习册系列答案
相关题目
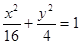 ,过点
,过点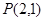 且被点
且被点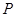 平分的椭圆的弦所在的直线方程是( )
平分的椭圆的弦所在的直线方程是( )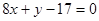
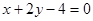
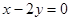
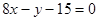
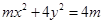 的离心率e为方程
的离心率e为方程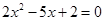 的两根,则满足条件的圆锥曲线的条数为 ( )
的两根,则满足条件的圆锥曲线的条数为 ( )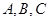 均在椭圆
均在椭圆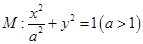 上,直线
上,直线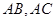 分别过椭圆的左、右焦点
分别过椭圆的左、右焦点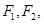 当
当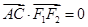 时,有
时,有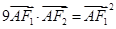
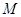 的方程
的方程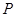 是椭圆
是椭圆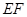 为圆
为圆 的任一条直径,求
的任一条直径,求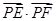 的最大值
的最大值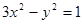 交于A,B两点.
交于A,B两点. 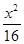
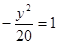 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,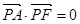
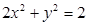 的一个焦点的直线交椭圆于
的一个焦点的直线交椭圆于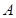 、
、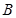 两点,求
两点,求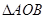 面积的最大值.(
面积的最大值.(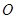 为坐标原点)
为坐标原点) ,若其长轴在
,若其长轴在 轴上.焦距为
轴上.焦距为 ,则
,则 等于___________。
等于___________。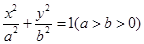 的一个焦点
的一个焦点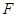 与抛物线
与抛物线 的焦点重合,P为椭圆与抛物线的一个公共点,且|PF|=2,倾斜角为
的焦点重合,P为椭圆与抛物线的一个公共点,且|PF|=2,倾斜角为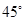 的直线
的直线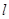 过点
过点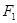 ,问抛物线
,问抛物线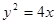 上是否存在一点
上是否存在一点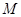 ,使得
,使得