题目内容
(Ⅰ)已知双曲线C与双曲线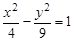 有相同的渐近线,且一条准线为
有相同的渐近线,且一条准线为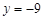 ,求双曲线C的方程;
,求双曲线C的方程;
 (Ⅱ)已知圆截
(Ⅱ)已知圆截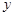 轴所得弦长为6,圆心在直线
轴所得弦长为6,圆心在直线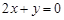 上,并与
上,并与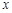 轴相切,求该圆的方程.
轴相切,求该圆的方程.
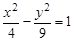 有相同的渐近线,且一条准线为
有相同的渐近线,且一条准线为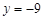 ,求双曲线C的方程;
,求双曲线C的方程; (Ⅱ)已知圆截
(Ⅱ)已知圆截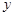 轴所得弦长为6,圆心在直线
轴所得弦长为6,圆心在直线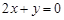 上,并与
上,并与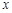 轴相切,求该圆的方程.
轴相切,求该圆的方程. (Ⅰ) ;(Ⅱ)
;(Ⅱ) 或
或 .
.
 ;(Ⅱ)
;(Ⅱ) 或
或 .
.试题分析:(Ⅰ)由题设双曲线C的方程为
 ,则
,则 ,
,∴ 双曲线C的方程为
 ;
; (Ⅱ)由题设圆的方程为
(Ⅱ)由题设圆的方程为 ,则
,则 ,
,∴ 圆的方程为
 或
或 .
.点评:已知渐近线方程为
 ,则可设渐近线方程为
,则可设渐近线方程为 ;与双曲线
;与双曲线 共渐近线的双曲线方程可设为:
共渐近线的双曲线方程可设为: 。
。
练习册系列答案
相关题目
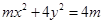 的离心率e为方程
的离心率e为方程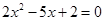 的两根,则满足条件的圆锥曲线的条数为 ( )
的两根,则满足条件的圆锥曲线的条数为 ( )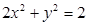 的一个焦点的直线交椭圆于
的一个焦点的直线交椭圆于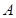 、
、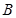 两点,求
两点,求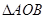 面积的最大值.(
面积的最大值.( 为坐标原点)
为坐标原点) ,若其长轴在
,若其长轴在 轴上.焦距为
轴上.焦距为 ,则
,则 等于___________。
等于___________。 的参数方程为
的参数方程为 ,以
,以 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 在极坐标系中的方程为
在极坐标系中的方程为 .若曲线
.若曲线 的取值范围是 .
的取值范围是 . 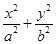 (a>b>0)的离心率
(a>b>0)的离心率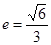 ,过点
,过点 和
和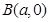 的直线与原点的距离为
的直线与原点的距离为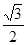 .
.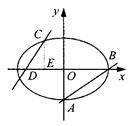
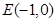 ,若直线
,若直线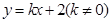 与椭圆交于
与椭圆交于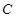 、
、 两 点.问:是否存在
两 点.问:是否存在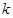 的值,
的值,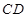 为直径的圆过
为直径的圆过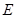 点?请说明理由.
点?请说明理由. 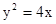 的焦点,与抛物线交与A、B两点,则
的焦点,与抛物线交与A、B两点,则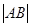 = .
= .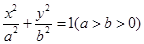 的一个焦点
的一个焦点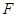 与抛物线
与抛物线 的焦点重合,P为椭圆与抛物线的一个公共点,且|PF|=2,倾斜角为
的焦点重合,P为椭圆与抛物线的一个公共点,且|PF|=2,倾斜角为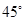 的直线
的直线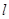 过点
过点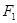 ,问抛物线
,问抛物线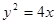 上是否存在一点
上是否存在一点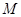 ,使得
,使得 ABC中,
ABC中, C=90°,AC="b," BC="a," P为三角形内的一点,且
C=90°,AC="b," BC="a," P为三角形内的一点,且 ,
,