Question

【题目】已知函数 ，a∈R．
（Ⅰ）当a∈[1，e2]时，讨论函数f（x）的零点的个数；
（Ⅱ）令g（x）=tx2﹣4x+1，t∈[﹣2，2]，当a∈[1，e]时，证明：对任意的 ，存在x2∈[0，1]，使得f（x1）=g（x2）．

Answer 1

【答案】解：（Ⅰ）f（x）的定义域是（0，+∞），f′（x）= ， 令f′（x）=0，解得：x= 或x=﹣ （舍），
x∈（0， ）时，f′（x）＞0，f（x）递增，
x∈（ ，+∞）时，f′（x）＜0，f（x）递减，
故f（x）max=f（ ）= a（lna﹣1），
令h（a）= a（lna﹣1），a∈[1，e2]，则h′（a）= lna≥0，
故函数h（a）在[1，e2]递增，
故h（1）≤h（a）≤h（e2），即﹣ ≤h（a）≤ e2 ，
令h（a）=0，则a=e，
a∈[1，e）时，h（a）＜0，即f（x）max＜0，此时f（x）无零点，
a=e时，h（a）=0，即f（x）max=0，f（x）有1个零点，
a∈（e，e2]时，h（a）＞0，即f（x）max＞0，
由函数f（x）的定义域可知x→0时，lnx→﹣∞，
x2→0，故f（x）→﹣∞，x→+∞时，f（x）→﹣∞，
故此时f（x）有2个零点，
综上，a∈[1，e）时，函数f（x）无零点，a=e时，函数f（x）有唯一零点，
a∈（e，e2]时，函数f（x）有2个零点；
（Ⅱ）由（Ⅰ）得：a∈[1，e]时，f（x）max=f（ ）≤0，又f（1）=﹣ ，
f（ ）= （a﹣e）∈[ （1﹣e），0]，
当 （a﹣e）≥﹣ 时，函数f（x）=alnx﹣ x2 ， （x∈[1， ）的值域是：
[﹣ ， a（lna﹣1）][﹣ ，0]，
当 （a﹣e）＜﹣ 时，函数f（x）=alnx﹣ x2（x∈[1， ]的值域是：
[ （a﹣e）， a（lna﹣1）][ （1﹣e）， a（lna﹣1）][﹣1，0]，
由上可知，对于任意的x1∈[1， ]，f（x1）∈[﹣1，0]，
对于函数g（x），g（x）=tx2﹣4x+1=t 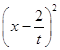+1﹣ ，x∈[0，1]，
当﹣2≤t＜0时， ＜0，g（x）在区间[0，1]递减，
当t=0时，g（x）=﹣4x+1，g（x）在区间[0，1]递减，
0＜t≤2时， ≥1，g（x）在区间[0，1]递减，
故t∈[﹣2，2]时，g（x）min=g（1）=t﹣3∈[﹣5，﹣1]，g（x）max=g（0）=1，
故x2∈[0，1]时，g（x2）∈[﹣1，0][t﹣3，1]，
故对任意的 ，存在x2∈[0，1]，使得f（x1）=g（x2）
【解析】（Ⅰ）求出函数的导数，解关于导函数的方程，求出函数的单调区间，求出函数的最大值，通过讨论a的范围，判断函数的零点个数即可；（Ⅱ）通过讨论a的范围，求出函数f（x）的值域，通过讨论t的范围，求出g（x）的最值，结合集合的包含关系证明结论即可．
【考点精析】关于本题考查的利用导数研究函数的单调性和函数的极值与导数，需要了解一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减；求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值才能得出正确答案．