题目内容
知a、b为实数，ab＞0，若函数f（x）=
+
sin
+a+b-1是奇函数，则f（1）的最小值是 ．
| x |
| a |
| 1 |
| b |
| πx |
| 2 |
考点：基本不等式,函数奇偶性的判断
专题：函数的性质及应用
分析：函数f（x）是奇函数，可得f（0）=0，化为a+b-1=0．再利用“乘1法”与基本不等式的性质即可得出．
解答：
解：∵函数f（x）是奇函数，
∴f（0）=0，化为a+b-1=0．
又ab＞0．
∴f（1）=
+
=（a+b）(
+
)=2+
+
≥2+2
=4，当且仅当a=b=
时取等号．
∴f（1）的最小值是4．
故答案为：4．
∴f（0）=0，化为a+b-1=0．
又ab＞0．
∴f（1）=
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| b |
| a |
| a |
| b |
|
| 1 |
| 2 |
∴f（1）的最小值是4．
故答案为：4．
点评：本题考查了函数的奇偶性、“乘1法”与基本不等式的性质，考查了推理能力与计算能力，属于基础题．
练习册系列答案
步步高达标卷系列答案
相关题目
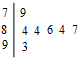如图是 a，b年在某大学自主招生面试环节中，七位评委为某考生打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为（ ）| A、83，1.5 |
| B、84，1.5 |
| C、85，1.6 |
| D、86，1.6 |
在△ABC中，三内角A、B、C所对的边分别为a、b、c，已知内角C为钝角，向量
=（2sinA，-1），
=（sinA，cos2A+2）且
⊥
．
（1）试求角A的大小；
（2）试比较b+c与
a的大小．
| m |
| n |
| m |
| n |
（1）试求角A的大小；
（2）试比较b+c与
| 3 |
函数f（x）=lnx-x+2的零点个数为（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
y=2cosx（
sinx+cosx）的一条对称轴为（ ）
| 3 |
A、x=
| ||
B、x=-
| ||
C、x=-
| ||
D、x=
|
给出以下四个命题：
（1）若x2-5x+6=0，则x=2或x=3；
（2）若2≤x＜3，则（x-2）（x-3）≤0；
（3）若a=b=0，则|a|+|b|=0；
（4）若x，y∈N，x+y是奇数，则x，y中一个是奇数，一个是偶数．
那么 （ ）
（1）若x2-5x+6=0，则x=2或x=3；
（2）若2≤x＜3，则（x-2）（x-3）≤0；
（3）若a=b=0，则|a|+|b|=0；
（4）若x，y∈N，x+y是奇数，则x，y中一个是奇数，一个是偶数．
那么 （ ）
| A、（4）的逆命题假 |
| B、（1）的逆命题真 |
| C、（2）的否命题真 |
| D、（3）的否命题假 |