题目内容
已知矩阵A=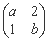 有一个属于特征值1的特征向量
有一个属于特征值1的特征向量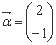 .
.
(Ⅰ) 求矩阵A;
(Ⅱ) 若矩阵B=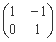 ,求直线
,求直线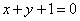 先在矩阵A,再在矩阵B的对应变换作用下的像的方程.
先在矩阵A,再在矩阵B的对应变换作用下的像的方程.
【解析】(Ⅰ)由已知得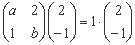 ,所以
,所以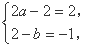 …………2分
…………2分
解得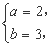 故A=
故A=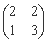 . ……………………………………………………3分
. ……………………………………………………3分
(Ⅱ) BA=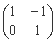
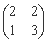 =
=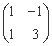 ,因为矩阵BA 所对应的线性变换将直线变成直线(或点),所以可取直线
,因为矩阵BA 所对应的线性变换将直线变成直线(或点),所以可取直线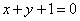 上的两点(0,1),(-1,2),……………………………4分
上的两点(0,1),(-1,2),……………………………4分
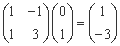 ,
,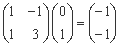 ,由得:(0,1),(-1,2)在矩阵A所对应的线性变换下的像是点(1,-3),(-1,-1) ……………………………6分
,由得:(0,1),(-1,2)在矩阵A所对应的线性变换下的像是点(1,-3),(-1,-1) ……………………………6分
从而直线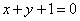 在矩阵BA所对应的线性变换下的像的方程为
在矩阵BA所对应的线性变换下的像的方程为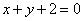 .…………7分
.…………7分

练习册系列答案
相关题目
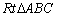 中,
中,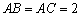 .如果一个椭圆通过
.如果一个椭圆通过 、
、 两点,它的一个焦点为点
两点,它的一个焦点为点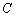 ,另一个焦点在边
,另一个焦点在边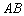 上,则这个椭圆的焦距为 .
上,则这个椭圆的焦距为 . 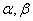 的法向量分别是
的法向量分别是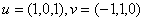 ,则这两个平面所成的锐二面角的度数是 。
,则这两个平面所成的锐二面角的度数是 。 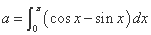 ,则二项式
,则二项式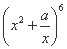 展开式中的
展开式中的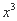 项的系数为( )
项的系数为( ) 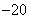 B. 20 C.
B. 20 C.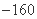 D. 160
D. 160 为1名顾客摸奖获得的奖金数额,求随机变量
为1名顾客摸奖获得的奖金数额,求随机变量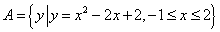 ,
,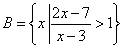 ,若任取
,若任取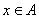 ,则
,则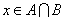 的概率为
的概率为 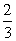 B.
B.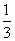 C.
C.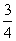 D.
D.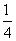
 是奇函数且
是奇函数且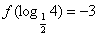 ,当
,当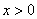 时,
时, 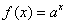 (
(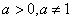 ),则
),则 的值为
的值为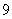 B.
B.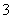 C.
C.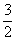 D.
D.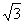
 ,则“
,则“ ”是“
”是“
 ,
, 的解集
的解集 .求
.求
 的值;
的值; 求
求 的最小值.
的最小值.