Question

3．已知函数f（x）=ax³+bx-1在x=1处有极小值-5．
（1）试求a，b的值，并求出f（x）的单调区间；
（2）若关于x的方程f（x）=2m-1有3个不同的实根，求实数m的取值范围．

Answer 1

分析 （1）求导，由题意可知：$\left\{\begin{array}{l}{f′（0）=0}\\{f（1）=-5}\end{array}\right.$，即可求得a和b的值；
（2）由（1）可知求得f（x）的极值，由题意可知，y=2m-1与f（x）有三个交点，即可求得实数m的取值范围．

解答 解：（1）求导，f′（x）=3ax²+b，
由题意可知$\left\{\begin{array}{l}{f′（0）=0}\\{f（1）=-5}\end{array}\right.$，则$\left\{\begin{array}{l}{3a+b=0}\\{a+b-1=-5}\end{array}\right.$，解得：$\left\{\begin{array}{l}{a=2}\\{b=-6}\end{array}\right.$，
则a=2，b=-6，
（2）由（1）可知：f（x）=2x³-6x-1，求导f′（x）=6x²-6，
令f′（x）=0，解得x=1或x=-1，
则x，f′（x），f（x）的变化如图所示：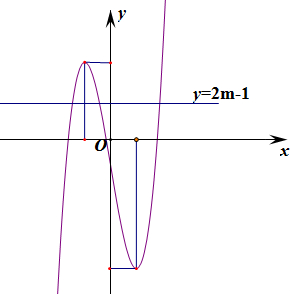

x	（-∞，-1）	-1	（-1，1）	1	（1，+∞）
f′（x）	+	0	-	0	+
f（x）	↑	极大值（3）	↓	极小值（-5）	↑

由x的方程f（x）=2m-1有3个不同的实根，
则y=2m-1与f（x）有三个交点，
则-5＜2m-1＜3，
解得：-2＜m＜2，
实数m的取值范围（-2，2）．

点评 本题考查导数的综合应用，考查利用导数求函数的单调性及极值，考查直线与函数的交点问题，属于中档题．