��Ŀ����
14��������ABCD-A1B1C1D1 ���ⳤΪ1��EΪA1B1 ���е㣬�������ĸ����⣺�ٵ�E��ƽ��ABC1D1 �ľ���Ϊ$\frac{1}{2}$��
��ֱ��BC��ƽ��ABC1D1 ���ɵĽǵ���45��
�ۿռ��ı���ABCD1 �����������������γ�������Ӱ���������Сֵ��$\frac{1}{2}$
��AE��DC���ɽǵ�����ֵΪ$\frac{\sqrt{5}}{5}$
����������ĸ����ǣ�������
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
���� �ڢ��У�E����ABC1D1�ľ������B1����ABC1D1�ľ���Ϊ$\frac{1}{2}$B1C���ڢ��У�BC����ABC1D1���ɵĽǼ�Ϊ��CBC1���ڢ��У����ĸ����ϵ�ͶӰ��Ϊ�����λ�Ϊ�����Σ���СΪ�����Σ��ڢ��У���EAB��AE��DC���ɽǣ�
��� �⣺�ڢ��У�E��A1B1��A1B1����ABC1D1��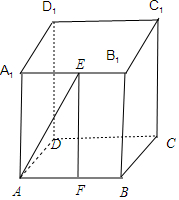 ��E����ABC1D1�ľ������B1����ABC1D1�ľ���Ϊ$\frac{1}{2}$B1C=$\frac{\sqrt{2}}{2}$���ʢٴ���
��E����ABC1D1�ľ������B1����ABC1D1�ľ���Ϊ$\frac{1}{2}$B1C=$\frac{\sqrt{2}}{2}$���ʢٴ���
�ڢ��У�BC����ABC1D1���ɵĽǼ�Ϊ��CBC1=45�㣬�ʢ���ȷ��
�ڢ��У����ĸ����ϵ�ͶӰ��Ϊ�����λ�Ϊ�����Σ���СΪ�����Σ����Ϊ$\frac{1}{2}$���ʢ���ȷ��
�ڢ��У���DC��AB�����EAB��AE��DC���ɽǣ�
ȡAB�е�F������EF����AF=$\frac{1}{2}$��AE=$\sqrt{1+\frac{1}{4}}=\frac{\sqrt{5}}{2}$��
��cos��EAB=$\frac{AF}{AE}$=$\frac{\frac{1}{2}}{\frac{\sqrt{5}}{2}}$=$\frac{\sqrt{5}}{5}$���ʢ���ȷ��
��ѡ��C��
���� ���⿼�����������жϣ�����������ṹ�������㵽ƽ��ľ��롢����ǡ�ͶӰ���������ֱ�����ɽǵȻ���֪ʶ������������֤��������������������������ν��˼�롢�����뷽��˼�롢������ת��˼�룬���е��⣮

| A�� | $y=4sin��4x+\frac{��}{6}��$ | B�� | $y=2sin��2x+\frac{��}{3}��+2$ | C�� | $y=2sin��4x+\frac{��}{3}��+2$ | D�� | $y=2sin��4x+\frac{��}{6}��+2$ |
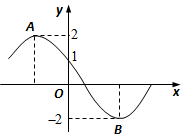 ��ͼ��ʾΪ����f��x��=2sin����x+�գ����أ�0��0�ܦաܦУ��IJ���ͼ������A��B����֮��ľ���Ϊ5����ôf��-1��=2��
��ͼ��ʾΪ����f��x��=2sin����x+�գ����أ�0��0�ܦաܦУ��IJ���ͼ������A��B����֮��ľ���Ϊ5����ôf��-1��=2��