题目内容
已知数列![]() ,其中
,其中![]() ,且
,且![]()
(Ⅰ)求![]() ;
;
(Ⅱ)求证:对任意![]() ,
,![]() .
.
(Ⅰ)解:![]()
![]() =6
=6
![]() n=1时,
n=1时,![]() =1,解得
=1,解得![]() =1
=1
(Ⅱ)证明:①n=1,2时,由上可知,![]() =n(2n-1)成立
=n(2n-1)成立
②假设n=k(k![]() 2,k
2,k![]() N+)时,ak=k(2k-1)成立
N+)时,ak=k(2k-1)成立
则对n=k+1,由![]() =k可得:
=k可得:
![]() =k(
=k(![]() )
)
(k-1)![]() =(k+1)
=(k+1)![]() -(k+1)
-(k+1)
=(k+1)(![]() -1)
-1)
=(k+1)(2k2-k-1)
=(k+1)(k-1)(2k+1)
![]() k
k![]() 2
2
![]()
![]() =(k+1)[2(k+1)-1)]
=(k+1)[2(k+1)-1)]
![]() n=k+1时成立
n=k+1时成立
由①②得,an=n(2n-1)对n![]() N+成立。
N+成立。

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
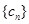 ,其中
,其中 ,且数列
,且数列 为等比数列,求常数p;
为等比数列,求常数p; 、
、 是公比不相等的两个等比数列,
是公比不相等的两个等比数列, ,证明:数列
,证明:数列