题目内容
(1)已知数列![]() ,其中
,其中![]() ,且数列
,且数列![]() 为等比数列,求常数p;
为等比数列,求常数p;
(2)设![]() 、
、![]() 是公比不相等的两个等比数列,
是公比不相等的两个等比数列,![]() ,证明:数列
,证明:数列![]() 不是等比数列.
不是等比数列.
解:(1)解:因为{cn+1-pcn}是等比数列,
故有:(cn+1-pcn)2=(cn+2-pcn+1)(cn-pcn-1),将cn=2n+3n代入上式,得:
[2n+1+3n+1-p(2n+3n)]2=[2n+2+3n+2-p(2n+1+3n+1)]·[2n+3n-p(2n-1+3n-1)],
即[(2-p)2n+(3-p)3n]2
=[(2-p)2n+1+(3-p)3n+1][(2-p)2n-1+(3-p)3n-1],
整理得![]() (2-p)(3-p)·2n·3n=0,解得p=2或p=3.
(2-p)(3-p)·2n·3n=0,解得p=2或p=3.
(2)证明:设{an}、{bn}的公比分别为p、q,p≠q,cn=an+bn.
为证{cn}不是等比数列只需证c22≠c1·c3.
事实上,c22=(a1p+b1q)2=a12p2+b12q2+2a1b1pq,
c1·c3=(a1+b1)(a1p2+b1q2)=a12p2+b12q2+a1b1(p2+q2),
由于p≠q,p2+q2>2pq,又a1、b1不为零,因此c22≠c1·c3,故{cn}不是等比数列.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
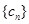 ,其中
,其中 ,且数列
,且数列 为等比数列,求常数p;
为等比数列,求常数p; 、
、 是公比不相等的两个等比数列,
是公比不相等的两个等比数列, ,证明:数列
,证明:数列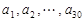 ,其中
,其中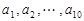 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;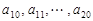 是公差为
是公差为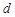 的等差数列;
的等差数列;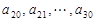 是公差为
是公差为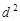 的等差数列(
的等差数列(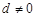 ).
).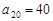 ,求
,求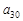 关于
关于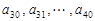 是公差为
是公差为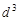 的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?