题目内容
在直角△ABC中,AB=2,AC=2
,斜边BC上有异于端点两点B、C的两点E、F,且EF=1,则
•
的取值范围是 .
| 3 |
| AE |
| AF |
考点:平面向量数量积的运算
专题:计算题,函数的性质及应用,平面向量及应用
分析:以A为坐标原点,AB、AC方向为x,y轴正方向建立坐标系,分别求出向量
、
的坐标,代入向量数量积的运算公式,由二次函数的值域求法即可得到所求范围.
| AE |
| AF |
解答:
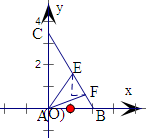 解:以A为坐标原点,AB、AC方向为x,y轴正方向建立坐标系.
解:以A为坐标原点,AB、AC方向为x,y轴正方向建立坐标系.
可得A(0,0),B(2,0),C(0,2
)
又EF=1,设E(m,
(2-m)),F(m+
,
(
-m)),(0≤m≤
),
则
=(m,
(2-m))),
=(m+
,
(
-m)),
即有
•
=m(m+
)+3(2-m)(
-m)=4m2-10m+9=4(m-
)2+
,
当m=
时,取得最小值
,当m=0时,取得最大值9.
即有所求取值范围是[
,9].
故答案为:[
,9].
 解:以A为坐标原点,AB、AC方向为x,y轴正方向建立坐标系.
解:以A为坐标原点,AB、AC方向为x,y轴正方向建立坐标系.可得A(0,0),B(2,0),C(0,2
| 3 |
又EF=1,设E(m,
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
则
| AE |
| 3 |
| AF |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
即有
| AE |
| AF |
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
| 11 |
| 4 |
当m=
| 5 |
| 4 |
| 11 |
| 4 |
即有所求取值范围是[
| 11 |
| 4 |
故答案为:[
| 11 |
| 4 |
点评:本题考查平面向量数量积的运算,将向量数量积的运算坐标化是解决问题的关键,属中档题.

练习册系列答案
相关题目
已知i是虚数单位,则
=( )
| i |
| 1-i |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
“x≠1且y≠2”是“x+y≠3”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
