题目内容
下列函数中,在[1,+∞)上为增函数的是( )
| A、y=(x-2)2 | ||
| B、y=|x-1| | ||
C、y=
| ||
| D、y=-(x+1)2 |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:结合A、B、C、D选项中四个函数的图象与性质进行判断,即可得出正确的答案.
解答:
解:对于A,函数y=(x-2)2的图象是抛物线,对称轴是x=2,当x<2时是减函数,x>2时是增函数,∴不满足题意;
对于B,函数y=|x-1|=
,∴当x≥1时,是增函数,x<1时,是减函数,∴满足题意;
对于C,函数y=
,当x<-1,x>-1时,函数是减函数,∴不满足题意;
对于D,函数y=-(x+1)2的图象是抛物线,对称轴是x=-1,当x>-1时是减函数,x<-1时是增函数,∴不满足题意;
故选:B.
对于B,函数y=|x-1|=
|
对于C,函数y=
| 1 |
| x+1 |
对于D,函数y=-(x+1)2的图象是抛物线,对称轴是x=-1,当x>-1时是减函数,x<-1时是增函数,∴不满足题意;
故选:B.
点评:本题考查了基本初等函数的单调性问题,解题时应根据选项中的每一个函数的图象与性质,进行分析与解答,是基础题.

练习册系列答案
相关题目
下列命题中:(1)若a>b,则lg
>0;(2)若a>b>0,则
<
;(3)若
>
,则ad>bc;(4)若a>b,c>d,则a-d>b-c.其中正确的命题有( )
| a |
| b |
| 1 |
| a |
| 1 |
| b |
| a |
| c |
| b |
| d |
| A、1个 | B、2个 | C、3个 | D、4个 |
在△ABC中,A=60°,C=45°,a=10,则边c的长为( )
A、5
| ||||
B、10
| ||||
C、
| ||||
D、5
|
| 5i2014 |
| 2-i |
| A、-2+i | B、-2-i |
| C、-1-2i | D、-1+2i |
在等差数列3,8,13…中,第5项为( )
| A、15 | B、18 | C、19 | D、23 |
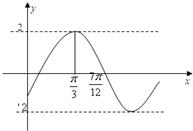 已知函数y=Asin(ωx+φ)(ω>0,A>0,|φ|<
已知函数y=Asin(ωx+φ)(ω>0,A>0,|φ|<| π |
| 2 |
A、y=sin(2x+
| ||
B、y=2sin(x-
| ||
C、y=2sin(2x-
| ||
D、y=2sin(2x+
|
定义在R上的函数f(x)的图象关于点(-
,0)成中心对称且对任意的实数x都有f(x)=-f(x+
)且f(-1)=1,f(0)=-2,则f(1)+f(2)+…+f(2014)=( )
| 3 |
| 4 |
| 3 |
| 2 |
| A、1 | B、0 | C、-1 | D、2 |
复数3i(3+4i)的虚部是( )
| A、9 | B、-12+9i |
| C、12 | D、9i |